
【题目】[选修4-1:几何证明选讲]
如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D点作DF⊥CE,垂足为F.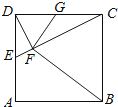
(1)证明:B,C,G,F四点共圆;
(2)若AB=1,E为DA的中点,求四边形BCGF的面积.
【答案】
(1)
证明:∵DF⊥CE,
∴Rt△DFC∽Rt△EDC,
∴ ![]() ,
,
∵DE=DG,CD=BC,
∴ ![]() ,
,
又∵∠GDF=∠DEF=∠BCF,
∴△GDF∽△BCF,
∴∠CFB=∠DFG,
∴∠GFB=∠GFC+∠CFB=∠GFC+∠DFG=∠DFC=90°,
∴∠GFB+∠GCB=180°,
∴B,C,G,F四点共圆.
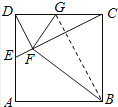
(2)
∵E为AD中点,AB=1,∴DG=CG=DE= ![]() ,
,
∴在Rt△DFC中,GF= ![]() CD=GC,连接GB,Rt△BCG≌Rt△BFG,
CD=GC,连接GB,Rt△BCG≌Rt△BFG,
∴S四边形BCGF=2S△BCG=2× ![]() ×1×
×1× ![]() =
= ![]() .
.
【解析】(1)证明B,C,G,F四点共圆可证明四边形BCGF对角互补,由已知条件可知∠BCD=90°,因此问题可转化为证明∠GFB=90°;(2)在Rt△DFC中,GF= ![]() CD=GC,因此可得△GFB≌△GCB,则S四边形BCGF=2S△BCG , 据此解答.;本题考查四点共圆的判断,主要根据对角互补进行判断,注意三角形相似和全等性质的应用.
CD=GC,因此可得△GFB≌△GCB,则S四边形BCGF=2S△BCG , 据此解答.;本题考查四点共圆的判断,主要根据对角互补进行判断,注意三角形相似和全等性质的应用.


科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 和等比数列
和等比数列![]() 满足
满足![]() ,
, ![]() ,
, ![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)求和: ![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据等差数列![]() 的
的![]() ,
, ![]() ,列出关于首项
,列出关于首项![]() 、公差
、公差![]() 的方程组,解方程组可得
的方程组,解方程组可得![]() 与
与![]() 的值,从而可得数列
的值,从而可得数列![]() 的通项公式;(2)利用已知条件根据题意列出关于首项
的通项公式;(2)利用已知条件根据题意列出关于首项![]() ,公比
,公比![]() 的方程组,解得
的方程组,解得![]() 、
、![]() 的值,求出数列
的值,求出数列![]() 的通项公式,然后利用等比数列求和公式求解即可.
的通项公式,然后利用等比数列求和公式求解即可.
试题解析:(1)设等差数列{an}的公差为d. 因为a2+a4=10,所以2a1+4d=10.解得d=2.
所以an=2n1.
(2)设等比数列的公比为q. 因为b2b4=a5,所以b1qb1q3=9.
解得q2=3.所以![]() .
.
从而![]() .
.
【题型】解答题
【结束】
18
【题目】已知命题![]() :实数
:实数![]() 满足
满足![]() ,其中
,其中![]() ;命题
;命题![]() :方程
:方程![]() 表示双曲线.
表示双曲线.
(1)若![]() ,且
,且![]() 为真,求实数
为真,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的4个图像中,与所给3个事件最吻合的顺序为
①我离开家后,心情愉快,缓慢行进,但最后发现快迟到时,加速前进;
②我骑着自行车上学,但中途车坏了,我修理好又以原来的速度前进;
③我快速的骑着自行车,最后发现时间充足,又减缓了速度.

① ② ③ ④
A. ③①② B. ③④② C. ②①③ D. ②④③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆![]() 的半径为2,点
的半径为2,点![]() 是圆
是圆![]() 的六等分点中的五个点.
的六等分点中的五个点.

(1)从![]() 中随机取三点构成三角形,求这三点构成的三角形是直角三角形的概率;
中随机取三点构成三角形,求这三点构成的三角形是直角三角形的概率;
(2)在圆![]() 上随机取一点
上随机取一点![]() ,求
,求![]() 的面积大于
的面积大于![]() 的概率
的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是双曲线
是双曲线![]() 上一点,
上一点, ![]() 分别是双曲线
分别是双曲线![]() 的左、右顶点,直线
的左、右顶点,直线![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求双曲线的离心率;
(2)过双曲线![]() 的右焦点且斜率为
的右焦点且斜率为![]() 的直线交双曲线于
的直线交双曲线于![]() 两点,
两点, ![]() 为坐标原点,
为坐标原点, ![]() 为双曲线上一点,满足
为双曲线上一点,满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
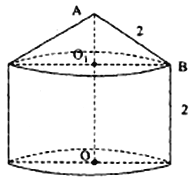
【题目】某粮库拟建一个储粮仓如图所示,其下部是高为2的圆柱,上部是母线长为2的圆锥,现要设计其底面半径和上部圆锥的高,若设圆锥的高![]() 为
为![]() ,储粮仓的体积为
,储粮仓的体积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;(圆周率用
的函数关系式;(圆周率用![]() 表示)
表示)
(2)求![]() 为何值时,储粮仓的体积最大.
为何值时,储粮仓的体积最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com