
【题目】如图,在三棱锥![]() 中,
中,![]() 是正三角形,
是正三角形,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() .
.
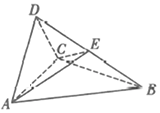
(1)证明:平面![]() 平面
平面![]() ;
;
(2)设![]() ,点
,点![]() 为
为![]() 的中点,求三棱锥
的中点,求三棱锥![]() 的体积.
的体积.
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将![]() 的方程化为普通方程,将
的方程化为普通方程,将![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数,且
为参数,且![]() ),
),![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求
,求![]() 的极坐标方程;
的极坐标方程;
(2)若![]() 与
与![]() 恰有4个公共点,求
恰有4个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节突如其来的新型冠状病毒肺炎在湖北爆发,一方有难八方支援,全国各地的白衣天使走上战场的第一线,某医院抽调甲、乙两名医生,抽调![]() 、
、![]() 、
、![]() 三名护士支援武汉第一医院与第二医院,参加武汉疫情狙击战其中选一名护士与一名医生去第一医院,其它都在第二医院工作,则医生甲和护士
三名护士支援武汉第一医院与第二医院,参加武汉疫情狙击战其中选一名护士与一名医生去第一医院,其它都在第二医院工作,则医生甲和护士![]() 被选在第一医院工作的概率为( )
被选在第一医院工作的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节突如其来的新型冠状病毒肺炎在湖北爆发,一方有难八方支援,全国各地的白衣天使走上战场的第一线,某医院抽调甲、乙两名医生,抽调![]() 、
、![]() 、
、![]() 三名护士支援武汉第一医院与第二医院,参加武汉疫情狙击战其中选一名护士与一名医生去第一医院,其它都在第二医院工作,则医生甲和护士
三名护士支援武汉第一医院与第二医院,参加武汉疫情狙击战其中选一名护士与一名医生去第一医院,其它都在第二医院工作,则医生甲和护士![]() 被选在第一医院工作的概率为( )
被选在第一医院工作的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E,F分别为B1C1,C1D1的中点,点P是上底面A1B1C1D1内一点,且AP∥平面EFDB,则cos∠APA1的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是边长为2的正方形.
是边长为2的正方形.![]() 平面
平面![]() ,且
,且![]() .
.
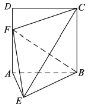
(1)求证:平面![]() 平面
平面![]() .
.
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使三棱锥
,使三棱锥![]() 的高
的高![]() 若存在,请求出
若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为解决城市的拥堵问题,某城市准备对现有的一条穿城公路MON进行分流,已知穿城公路MON自西向东到达城市中心点O后转向东北方向(即![]() ).现准备修建一条城市高架道路L,L在MO上设一出入口A,在ON上设一出入口B.假设高架道路L在AB部分为直线段,且要求市中心O与AB的距离为10km.
).现准备修建一条城市高架道路L,L在MO上设一出入口A,在ON上设一出入口B.假设高架道路L在AB部分为直线段,且要求市中心O与AB的距离为10km.
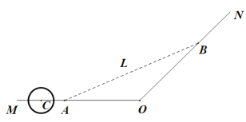
(1)求两站点A,B之间距离的最小值;
(2)公路MO段上距离市中心O30km处有一古建筑群C,为保护古建筑群,设立一个以C为圆心,5km为半径的圆形保护区.则如何在古建筑群C和市中心O之间设计出入口A,才能使高架道路L及其延伸段不经过保护区(不包括临界状态)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com