
(本小题满分12分)已知函数 的图象在点
的图象在点 处的切线方程为
处的切线方程为 .
.
(1)用 表示出
表示出 ;
;
(2)若 在
在 上恒成立,求
上恒成立,求 的取值范围;
的取值范围;
(3)证明: .
.
【解析】(Ⅰ) ,则有
,则有 ,解得
,解得  ….3分
….3分
(Ⅱ)由(Ⅰ)知, ,
,
令 ,
,
则  ,
, ………….5分
………….5分
(i)当
 ,
,
若  ,则
,则 ,
,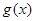 是减函数,所以
是减函数,所以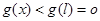
 ,故
,故 在
在 上恒不成立。
上恒不成立。
(ii) 时,
时, ………………………………….7分
………………………………….7分
若 ,故当
,故当 时,
时, 综上所述,
综上所述,
所求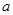 的取值范围为
的取值范围为
(Ⅲ)解法一:由(Ⅱ)知:当 时,有
时,有 。
。
令 ,有
,有
当 时,
时,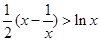 。…………………………8分
。…………………………8分
令 ,有
,有
即 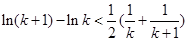 ,
,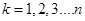 …………………….10分
…………………….10分
将上述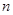 个不等式一次相加得
个不等式一次相加得

整理得: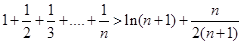 …………………….12分
…………………….12分
解法二:用数学归纳法证明
(1)当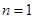 时,左边
时,左边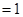 ,右边
,右边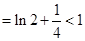 ,不等式成立…………….8分
,不等式成立…………….8分
(2)假设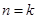 时, 不等式成立, 就是
时, 不等式成立, 就是

那么
 ………………………………….9分
………………………………….9分
由(Ⅱ)知:当 时,有
时,有
令 ,有
,有 …………………………10分
…………………………10分
令 ,得:
,得: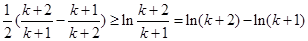

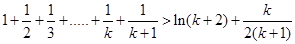 ………………………12分
………………………12分
就是说, 当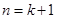 时,不等式也成立。
时,不等式也成立。
根据(1)和(2),可知不等式对任何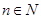 都成立。
都成立。


科目:高中数学 来源: 题型:
| ON |
| ON |
| 5 |
| OM |
| OT |
| M1M |
| N1N |
| OP |
| OA |
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009湖南卷文)(本小题满分12分)
为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目的个数分别占总数的![]() 、
、![]() 、
、![]() .现有3名工人独立地从中任选一个项目参与建设.求:
.现有3名工人独立地从中任选一个项目参与建设.求:
(I)他们选择的项目所属类别互不相同的概率; w.w.w.k.s.5.u.c.o.m ![]()
![]()
(II)至少有1人选择的项目属于民生工程的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2,
(注:利润与投资单位是万元)
(1)分别将A,B两种产品的利润表示为投资的函数,并写出它们的函数关系式.(2)该企业已筹集到10万元资金,并全部投入到A,B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com