
【题目】2019年4月,甲乙两校的学生参加了某考试机构举行的大联考,现对这两校参加考试的学生的数学成绩进行统计分析,数据统计显示,考生的数学成绩![]() 服从正态分布
服从正态分布![]() ,从甲乙两校100分及以上的试卷中用系统抽样的方法各抽取了20份试卷,并将这40份试卷的得分制作成如图所示的茎叶图:
,从甲乙两校100分及以上的试卷中用系统抽样的方法各抽取了20份试卷,并将这40份试卷的得分制作成如图所示的茎叶图:
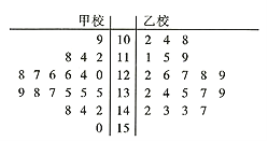
(1)试通过茎叶图比较这40份试卷的两校学生数学成绩的中位数;
(2)若把数学成绩不低于135分的记作数学成绩优秀,根据茎叶图中的数据,判断是否有![]() 的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关?
的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关?
(3)从所有参加此次联考的学生中(人数很多)任意抽取3人,记数学成绩在134分以上的人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]()
![]() ,
,![]() .
.
参考公式与临界值表:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【答案】(1)甲![]() ,乙
,乙![]() ;(2)没有90%的把握;(3)
;(2)没有90%的把握;(3)![]() .
.
【解析】
(1)由茎叶图的中位数计算即可;
(2)得2×2列联表,再根据表中数据计算K2,结合临界值表可得;
(3)因为![]() ,所以
,所以![]() ,,由题意可知
,,由题意可知![]() ,计算
,计算![]() 即可.
即可.
(1)由茎叶图可知:甲校学生数学成绩的中位数为![]() ,乙校学生数学成绩的中位数为
,乙校学生数学成绩的中位数为![]() ,所以这40份试卷的成绩,甲校学生数学成绩的中位数比乙校学生数学成绩的中位数高.
,所以这40份试卷的成绩,甲校学生数学成绩的中位数比乙校学生数学成绩的中位数高.
(2)由题意,作出![]() 列联表如下:
列联表如下:
甲校 | 乙校 | 合计 | |
数学成绩优秀 | 10 | 7 | 17 |
数学成绩不优秀 | 10 | 13 | 23 |
合计 | 20 | 20 | 40 |
计算得![]() 的观测值
的观测值![]() ,
,
所以没有90![]() 的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关.
的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关.
(3)因为![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() ,
,
由题意可知![]() ,所以
,所以![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)讨论函数![]() 的单调性;
的单调性;
(3)若对于任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点![]() 的距离之比为定值
的距离之比为定值![]() 的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆在平面直角坐标系
的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆在平面直角坐标系![]() 中,
中,![]() 点
点![]() .设点
.设点![]() 的轨迹为
的轨迹为![]() ,下列结论正确的是( )
,下列结论正确的是( )
A. ![]() 的方程为
的方程为![]()
B. 在![]() 轴上存在异于
轴上存在异于![]() 的两定点
的两定点![]() ,使得
,使得![]()
C. 当![]() 三点不共线时,射线
三点不共线时,射线![]() 是
是![]() 的平分线
的平分线
D. 在![]() 上存在点
上存在点![]() ,使得
,使得![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若存在数列
,若存在数列![]() 满足
满足![]() (
(![]() ),则称数列
),则称数列![]() 是
是![]() 的“倒差数列”,下列关于“倒差数列”描述正确的是( )
的“倒差数列”,下列关于“倒差数列”描述正确的是( )
A.若数列![]() 是单增数列,但其“倒差数列”不一定是单增数列;
是单增数列,但其“倒差数列”不一定是单增数列;
B.若![]() ,则其“倒差数列”有最大值;
,则其“倒差数列”有最大值;
C.若![]() ,则其“倒差数列”有最小值;
,则其“倒差数列”有最小值;
D.若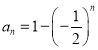 ,则其“倒差数列”有最大值.
,则其“倒差数列”有最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着互联网金融的不断发展,很多互联网公司推出余额增值服务产品和活期资金管理服务产品,如蚂蚁金服旗下的“余额宝”,腾讯旗下的“财富通”,京东旗下“京东小金库”.为了调查广大市民理财产品的选择情况,随机抽取1200名使用理财产品的市民,按照使用理财产品的情况统计得到如下频数分布表:
分组 | 频数(单位:名) |
使用“余额宝” |
|
使用“财富通” |
|
使用“京东小金库” | 30 |
使用其他理财产品 | 50 |
合计 | 1200 |
已知这1200名市民中,使用“余额宝”的人比使用“财富通”的人多160名.
(1)求频数分布表中![]() ,
,![]() 的值;
的值;
(2)已知2018年“余额宝”的平均年化收益率为![]() ,“财富通”的平均年化收益率为
,“财富通”的平均年化收益率为![]() .若在1200名使用理财产品的市民中,从使用“余额宝”和使用“财富通”的市民中按分组用分层抽样方法共抽取7人,然后从这7人中随机选取2人,假设这2人中每个人理财的资金有10000元,这2名市民2018年理财的利息总和为
.若在1200名使用理财产品的市民中,从使用“余额宝”和使用“财富通”的市民中按分组用分层抽样方法共抽取7人,然后从这7人中随机选取2人,假设这2人中每个人理财的资金有10000元,这2名市民2018年理财的利息总和为![]() ,求
,求![]() 的分布列及数学期望.注:平均年化收益率,也就是我们所熟知的利息,理财产品“平均年化收益率为
的分布列及数学期望.注:平均年化收益率,也就是我们所熟知的利息,理财产品“平均年化收益率为![]() ”即将100元钱存入某理财产品,一年可以获得3元利息.
”即将100元钱存入某理财产品,一年可以获得3元利息.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为改进服务质量,在进场购物的顾客中随机抽取了![]() 人进行问卷调查.调查后,就顾客“购物体验”的满意度统计如下:
人进行问卷调查.调查后,就顾客“购物体验”的满意度统计如下:
满意 | 不满意 | |
男 |
|
|
女 |
|
|
![]() 是否有
是否有![]() 的把握认为顾客购物体验的满意度与性别有关?
的把握认为顾客购物体验的满意度与性别有关?
![]() 若在购物体验满意的问卷顾客中按照性别分层抽取了
若在购物体验满意的问卷顾客中按照性别分层抽取了![]() 人发放价值
人发放价值![]() 元的购物券.若在获得了
元的购物券.若在获得了![]() 元购物券的
元购物券的![]() 人中随机抽取
人中随机抽取![]() 人赠其纪念品,求获得纪念品的
人赠其纪念品,求获得纪念品的![]() 人中仅有
人中仅有![]() 人是女顾客的概率.
人是女顾客的概率.
附表及公式: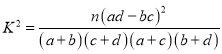 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右顶点为
的右顶点为![]() ,
,![]() 为上顶点,点
为上顶点,点![]() 为椭圆
为椭圆![]() 上一动点.
上一动点.
(1)若![]() ,求直线
,求直线![]() 与
与![]() 轴的交点坐标;
轴的交点坐标;
(2)设![]() 为椭圆
为椭圆![]() 的右焦点,过点
的右焦点,过点![]() 与
与![]() 轴垂直的直线为
轴垂直的直线为![]() ,
,![]() 的中点为
的中点为![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,求证:直线
,求证:直线![]() 与直线
与直线![]() 的交点在椭圆
的交点在椭圆![]() 上.
上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com