
【题目】在甲、乙两个盒子中分别装有编号为1,2,3,4的四个形状相同的小球,现从甲、乙两个盒子中各取出2个小球,每个小球被取出的可能性相等.
(1)求从甲盒中取出的两个球上的编号不都是奇数的概率;
(2)求从甲盒取出的小球上编号之和与从乙盒中取出的小球上编号之和相等的概率.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)任取2球的基本事件总数为6,用列举法列出事件“从甲盒中取出的两个球上的编号不都是奇数”所含的基本事件,计数后可得概率;
(2)由(1)知从甲,乙两个盒子中各取2个小球的基本事件总数为![]() 36,用列举法列出事件“从甲盒取出的小球上编号之和与从乙盒中取出的小球上编号之和相等”所含有的基本事件,计数后可计算概率.
36,用列举法列出事件“从甲盒取出的小球上编号之和与从乙盒中取出的小球上编号之和相等”所含有的基本事件,计数后可计算概率.
解:(1)记“从甲盒中取出的两个球上的编号不都是奇数”为事件A,由题意可知,从甲盒中取2个小球的基本事件总数为6,则事件A的基本事件有:
(1,2),(1,4),(2,3),(2,4),(3,4),共5个.∴P(A)=![]() .
.
(2)由题意可知,记“从甲盒取出的小球上编号之和与从乙盒中取出的小球上编号之和相等”为事件B,由题意可知,从甲,乙两个盒子中各取2个小球的基本事件总数为36,则事件B包含:(12,12),(13,13),(14,14),(14,23),(23,14),(23,23),(24,24),(34,34),共8个基本事件.∴P(B)=![]() .
.


科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在
,若存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点,已知函数
的不动点,已知函数![]()
(1)当![]() ,
,![]() 时,求函数
时,求函数![]() 的不动点;
的不动点;
(2)若对任意实数![]() ,函数
,函数![]() 恒有不动点,求
恒有不动点,求![]() 的取值范围;
的取值范围;
(3)在(2)条件下,若![]() 图象上的
图象上的![]() 两点的横坐标是函数
两点的横坐标是函数![]() 的不动点,且
的不动点,且![]() 的中点在直线
的中点在直线![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,在矩形
,在矩形![]() 中,
中, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起到
折起到![]() ,使得平面
,使得平面![]() 平面
平面![]() (如图
(如图![]() ).
).


图1 图2
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,对任意的正整数n,都有Sn=![]() an+n-3成立.
an+n-3成立.
(1)求证:存在实数λ使得数列{an+λ}为等比数列;
(2)求数列{nan}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“冰桶挑战赛”是一项社交网络上发起的慈善公益活动,活动规定:被邀请者要么在![]() 小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外
小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外![]() 个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(1)若某参与者接受挑战后,对其他![]() 个人发出邀请,则这
个人发出邀请,则这![]() 个人中至少有
个人中至少有![]() 个人接受挑战的概率是多少?
个人接受挑战的概率是多少?
(2)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构进行了随机抽样调查,调查得到如下列联表:
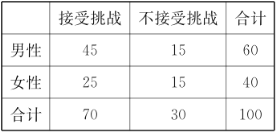
根据表中数据,能否有![]() %的把握认为“冰桶挑战赛与受邀者的性别有关”?
%的把握认为“冰桶挑战赛与受邀者的性别有关”?
附: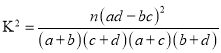

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=![]() ,an+1=3an-1(n∈N*).
,an+1=3an-1(n∈N*).
(1)若数列{bn}满足bn=an-![]() ,求证:{bn}是等比数列;
,求证:{bn}是等比数列;
(2)求数列{an}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年10月,举世瞩目的中国共产党第十九次全国代表大会在北京顺利召开.某高中为此组织全校2000名学生进行了一次“十九大知识知多少”的问卷测试(满分:100分),并从中抽取了40名学生的测试成绩,得到了如图所示的频率分布直方图.

(1)求图中实数![]() 的值及样本中40名学生测试成绩的平均数和中位数(同一组中的数据用该组区间的中点值作代表);
的值及样本中40名学生测试成绩的平均数和中位数(同一组中的数据用该组区间的中点值作代表);
(2)(i)利用分层抽样的方法从成绩低于70分的三组学生中抽取7人,再从这7人中随机抽取2人分析成绩不理想的原因,求前2组中至少有1人被抽到的概率;
(2)以频率估计概率,试估计该校这次测试成绩不低于80分的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com