
数列![]() ,
,![]() (
(![]() )由下列条件确定:①
)由下列条件确定:①![]() ;②当
;②当![]() 时,
时,![]() 与
与![]() 满足:当
满足:当![]() 时,
时,![]() ,
,![]() ;当
;当![]() 时,
时,![]() ,
,![]() .
.
(Ⅰ)若![]() ,
,![]() ,写出
,写出![]() ,并求数列
,并求数列![]() 的通项公式;
的通项公式;
(Ⅱ)在数列![]() 中,若
中,若![]() (
(![]() ,且
,且![]() ),试用
),试用![]() 表示
表示![]()
![]() ;
;
(Ⅲ)在(Ⅰ)的条件下,设数列![]()
![]() 满足
满足![]() ,
,![]() ,
,
![]() (其中
(其中![]() 为给定的不小于2的整数),求证:当
为给定的不小于2的整数),求证:当![]() 时,恒有
时,恒有![]() .
.
解: (Ⅰ)由题得过两点![]() ,
,![]() 直线
直线![]() 的方程为
的方程为![]() .………… 1分
.………… 1分
因为![]() ,所以
,所以![]() ,
,![]() .
.
设椭圆方程为![]() ,
,
由 消去
消去![]() 得,
得,![]() .
.
又因为直线![]() 与椭圆
与椭圆![]() 相切,所以
相切,所以![]() ,解得
,解得![]() .
.
所以椭圆方程为![]() . ……………………………………………… 5分
. ……………………………………………… 5分
(Ⅱ)易知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,…………………… 6分
,…………………… 6分
由 消去
消去![]() ,整理得
,整理得![]() . ………… 7分
. ………… 7分
由题意知![]() ,
,
解得![]() . ……………………………………………………………… 8分
. ……………………………………………………………… 8分
设![]() ,
,![]() ,则
,则![]() ,
,![]() . …… 9分
. …… 9分
又直线![]() 与椭圆
与椭圆![]() 相切,
相切,
由 解得
解得![]() ,所以
,所以![]() . ……………………………10分
. ……………………………10分
则![]() . 所以
. 所以![]() .
.
又![]()
![]()
![]()
![]()
![]()
![]()
所以![]() ,解得
,解得![]() .经检验成立. …………………… 13分
.经检验成立. …………………… 13分
所以直线![]() 的方程为
的方程为![]() . …………………… 14分
. …………………… 14分


科目:高中数学 来源:2011-2012学年北京市朝阳区高三上学期期末考试理科数学 题型:解答题
(本题满分14分)
数列 ,
, (
( )由下列条件确定:①
)由下列条件确定:① ;②当
;②当 时,
时, 与
与 满足:当
满足:当 时,
时, ,
, ;当
;当 时,
时, ,
, .
.
(Ⅰ)若 ,
, ,写出
,写出 ,并求数列
,并求数列 的通项公式;
的通项公式;
(Ⅱ)在数列 中,若
中,若 (
(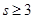 ,且
,且 ),试用
),试用 表示
表示
 ;
;
(Ⅲ)在(Ⅰ)的条件下,设数列
 满足
满足 ,
, ,
,
 (其中
(其中 为给定的不小于2的整数),求证:当
为给定的不小于2的整数),求证:当 时,恒有
时,恒有 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
数列![]() ,
,![]() (
(![]() )由下列条件确定:①
)由下列条件确定:①![]() ;②当
;②当![]() 时,
时,![]() 与
与![]() 满足:当
满足:当![]() 时,
时,![]() ,
,![]() ;当
;当![]() 时,
时,![]() ,
,![]() .
.
(Ⅰ)若![]() ,
,![]() ,求
,求![]() ,
,![]() ,
,![]() ,并猜想数列
,并猜想数列![]() 的通项公式(不需要证明);
的通项公式(不需要证明);
(Ⅱ)在数列![]() 中,若
中,若![]() (
(![]() ,且
,且![]() ),试用
),试用![]() 表示
表示![]() ,
,![]() ;
;
(Ⅲ)在(Ⅰ)的条件下,设数列![]()
![]() 满足
满足![]() ,
,![]() ,
,![]() (其中
(其中![]() 为给定的不小于2的整数),求证:当
为给定的不小于2的整数),求证:当![]() 时,恒有
时,恒有![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com