
【题目】已知函数f(x)=2lnx+x2﹣2ax(a>0). (I)讨论函数f(x)的单调性;
(Ⅱ)若函数f(x)有两个极值点x1 , x2(x1<x2),且f(x1)﹣f(x2)≥ ![]() ﹣2ln2恒成立,求a的取值范围.
﹣2ln2恒成立,求a的取值范围.
【答案】解:(Ⅰ)函数f(x)的定义域是(0,+∞),
f′(x)= ![]() ,令x2﹣ax+1=0,则△=a2﹣4,
,令x2﹣ax+1=0,则△=a2﹣4,
①0<a≤2时,△≤0,f′(x)≥0恒成立,
函数f(x)在(0,+∞)递增;
②a>2时,△>0,方程x2﹣ax+1=0有两根
x1= ![]() ,x2=
,x2= ![]() ,且0<x1<x2,
,且0<x1<x2,
函数f(x)在(0,x1)上f′(x)>0,
在(x1,x2)上,f′(x)<0,在(x2,+∞)上,f′(x)>0,
故函数f(x)在(0, ![]() )递增,在(
)递增,在( ![]() ,
, ![]() )递减,在(
)递减,在( ![]() ,+∞)递增;
,+∞)递增;
(Ⅱ)由(Ⅰ)得f(x)在(x1,x2)上递减,x1+x2=a,x1x2=1,
则f(x1)﹣f(x2)=2ln ![]() +(x1﹣x2)(x1+x2﹣2a)=2ln
+(x1﹣x2)(x1+x2﹣2a)=2ln ![]() +
+ ![]() ﹣
﹣ ![]() ,
,
令t= ![]() ,则0<t<1,f(x1)﹣f(x2)=2lnt+
,则0<t<1,f(x1)﹣f(x2)=2lnt+ ![]() ﹣t,
﹣t,
令g(t)=2lnt+ ![]() ﹣t,则g′(t)=﹣
﹣t,则g′(t)=﹣ ![]() <0,
<0,
故g(t)在(0,1)递减且g( ![]() )=
)= ![]() ﹣2ln2,
﹣2ln2,
故g(t)=f(x1)﹣f(x2)≥ ![]() ﹣2ln2=g(
﹣2ln2=g( ![]() ),即0<t≤
),即0<t≤ ![]() ,
,
而a2= ![]() =
= ![]() +
+ ![]() +2=t+
+2=t+ ![]() +2,其中0<t≤
+2,其中0<t≤ ![]() ,
,
∵(t+ ![]() +2)′=1﹣
+2)′=1﹣ ![]() ≤0在t∈(0,
≤0在t∈(0, ![]() ]恒成立,
]恒成立,
故a2=t+ ![]() +2在(0,
+2在(0, ![]() ]递减,
]递减,
从而a的范围是a2≥ ![]() ,
,
故a≥ ![]()
【解析】(Ⅰ)求出函数的导数,通过讨论a的范围求出函数的单调区间即可;(Ⅱ)得到x1+x2=a,x1x2=1,则f(x1)﹣f(x2)=2ln ![]() +(x1﹣x2)(x1+x2﹣2a)=2ln
+(x1﹣x2)(x1+x2﹣2a)=2ln ![]() +
+ ![]() ﹣
﹣ ![]() ,令t=
,令t= ![]() ,则0<t<1,f(x1)﹣f(x2)=2lnt+
,则0<t<1,f(x1)﹣f(x2)=2lnt+ ![]() ﹣t,令g(t)=2lnt+
﹣t,令g(t)=2lnt+ ![]() ﹣t,根据函数的单调性求出a的范围即可.
﹣t,根据函数的单调性求出a的范围即可.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】已成椭圆 ![]() 的左右顶点分别为
的左右顶点分别为 ![]() ,上下顶点分别为
,上下顶点分别为 ![]() ,左右焦点分别为
,左右焦点分别为 ![]() ,其中长轴长为4,且圆
,其中长轴长为4,且圆 ![]() 为菱形
为菱形 ![]() 的内切圆.
的内切圆.
(1)求椭圆 ![]() 的方程;
的方程;
(2)点 ![]() 为
为 ![]() 轴正半轴上一点,过点
轴正半轴上一点,过点 ![]() 作椭圆
作椭圆 ![]() 的切线
的切线 ![]() ,记右焦点
,记右焦点 ![]() 在
在 ![]() 上的射影为
上的射影为 ![]() ,若
,若 ![]() 的面积不小于
的面积不小于 ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个集合A,B,满足BA.若对任意的x∈A,存在ai , aj∈B(i≠j),使得x=λ1ai+λ2aj(λ1 , λ2∈{﹣1,0,1}),则称B为A的一个基集.若A={1,2,3,4,5,6,7,8,9,10},则其基集B元素个数的最小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的离心率为
的离心率为 ![]() ,M为C上除长轴顶点外的一动点,以M为圆心,
,M为C上除长轴顶点外的一动点,以M为圆心, ![]() 为半径作圆,过原点O作圆M的两条切线,A、B为切点,当M为短轴顶点时∠AOB=
为半径作圆,过原点O作圆M的两条切线,A、B为切点,当M为短轴顶点时∠AOB= ![]() . (Ⅰ)求椭圆的方程;
. (Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆的右焦点为F,过点F作MF的垂线交直线x= ![]() a于N点,判断直线MN与椭圆的位置关系.
a于N点,判断直线MN与椭圆的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且2Sn=4an﹣1. (Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=anan+1﹣2,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,若这200名学生中每周的自习时间不超过m小时的人数为164,则m的值约为( ) 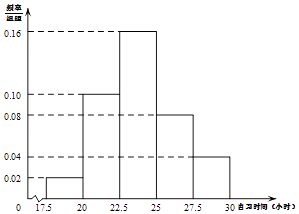
A.26.25
B.26.5
C.26.75
D.27
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°. 
(1)求证:BD⊥平面ADG;
(2)求此多面体的全面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】宿州市某登山爱好者为了解山高y(百米)与气温x(℃)之间的关系,随机统计了4次山高与相应的气温,并制作了对照表,由表中数据,得到线性回归方程为y=﹣2x+a,由此估计山高为72(百米)处的气温为( )
气温x(℃) | 18 | 13 | 10 | ﹣1 |
山高y(百米) | 24 | 34 | 38 | 64 |
A.﹣10
B.﹣8
C.﹣6
D.﹣4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com