
����Ŀ��ijУ�߶���20���50��ѧ���������п����У�ÿλͬѧ����ѧ���Է�����������![]() �ڣ����ð�����ͬѧ�Ŀ��Է�����Ϊ�߸��飺
�ڣ����ð�����ͬѧ�Ŀ��Է�����Ϊ�߸��飺![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����Ƴ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
�����Ƴ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.

��1������Ƶ�ʷֲ�ֱ��ͼ��������ο���ѧ���ɼ�����λ����ƽ������
��2����֪�ɼ�Ϊ104�ֻ�105�ֵ�ͬѧ����3�ˣ��ִӳɼ���![]() �е�ͬѧ����ѡ2�ˣ���������1�˳ɼ�������106�ֵĸ���Ϊ���٣���ÿλͬѧ�ijɼ���Ϊ������
�е�ͬѧ����ѡ2�ˣ���������1�˳ɼ�������106�ֵĸ���Ϊ���٣���ÿλͬѧ�ijɼ���Ϊ������
���𰸡���1����λ��Ϊ114��ƽ����Ϊ114.32����2��![]()
��������
��������λ�������߸�����ȣ����������λ������ÿ����м�ֵ���Ը����Ƶ������ͼ������ƽ������
����������������ɼ���![]() ���������Գɼ�Ϊ104�ֻ�105�ֵ�ͬѧ�ͳɼ�Ϊ106�֡�107�ֵ�ѧ����ţ����оٷ���Ϲŵ���͵ĸ��ʼ��㹫ʽ����������.
���������Գɼ�Ϊ104�ֻ�105�ֵ�ͬѧ�ͳɼ�Ϊ106�֡�107�ֵ�ѧ����ţ����оٷ���Ϲŵ���͵ĸ��ʼ��㹫ʽ����������.
������Ƶ�ʷֲ�ֱ��ͼ��֪![]() ������ѧ���ɼ�����λ��Ϊ
������ѧ���ɼ�����λ��Ϊ![]() .
.
ƽ����Ϊ![]()
![]() .
.
������Ϊ![]() �����Գɼ���
�����Գɼ���![]() ֮���ѧ������6��.
֮���ѧ������6��.
��ɼ�Ϊ104�֡�105�ֵ�ѧ��Ϊ![]() ��
��![]() ��
��![]() ���ɼ�Ϊ106�֡�107�ֵ�ѧ��Ϊ
���ɼ�Ϊ106�֡�107�ֵ�ѧ��Ϊ![]() ��
��![]() ��
��![]() .��6������ѡ2�ˣ�����
.��6������ѡ2�ˣ�����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() 15�����������ǡ��2�˶�������106�ֵ���
15�����������ǡ��2�˶�������106�ֵ���![]() ��
��![]() ��
��![]() ��3�������������1�˲�����106��1�˵���106�ֵ���
��3�������������1�˲�����106��1�˵���106�ֵ���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��9�ˣ����Դӳɼ���
��9�ˣ����Դӳɼ���![]() �е�ͬѧ����ѡ2�ˣ���������1�˳ɼ���������106�ֵĸ���Ϊ
�е�ͬѧ����ѡ2�ˣ���������1�˳ɼ���������106�ֵĸ���Ϊ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1����֪f��x����ͼ�����ԭ��Գƣ���ʵ��![]() ��ֵ��
��ֵ��
��2����![]() ����֪����
����֪����![]() ���㣺
���㣺![]() ������
������![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=��alnx+��a+1��x��![]() ��a��0����
��a��0����
��1�����ۺ���f��x���ĵ����ԣ�
��2����f��x���ݩ�![]() +ax+b���������a
+ax+b���������a![]() ʱ��ʵ��b�����ֵ��
ʱ��ʵ��b�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ũ���������棬�ٽ���ʳ������ȷ��������ʳ��ȫ���������ũ����ʳ�����Ļ����ԣ���2004�꿪ʼ������ʵʩ�˶�����ũ��ֱ�Ӳ���.ͨ����2014��2018������ݽ��е��飬����ij����������ʳ������![]() ����Ԫ����õ�����ʳ����
����Ԫ����õ�����ʳ����![]() �����ڶ֣�֮�������������ع�ϵ.ͳ���������±���
�����ڶ֣�֮�������������ع�ϵ.ͳ���������±���
��� | 2014�� | 2015�� | 2016�� | 2017�� | 2018�� |
������ | 9 | 10 | 12 | 11 | 8 |
��ʳ���� | 23 | 25 | 30 | 26 | 21 |
��1�������������������ݣ����![]() ����
����![]() �����Իع�ֱ�߷���
�����Իع�ֱ�߷���![]() ��
��
��2��ͨ���Ըõ�����ʳ�����ķ����о����ƻ�2019���ڸõ���������ʳ������7��Ԫ������ݣ�1�������õ����Իع�ֱ�߷��̣�Ԥ��2019��õ�������ʳ����.
���ο���ʽ��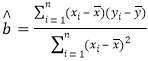 ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ![]() ���ҽ���Ϊ
���ҽ���Ϊ![]() ��
��![]() ΪԲ
ΪԲ![]() ����Բ
����Բ![]() ��һ�������㣬
��һ�������㣬![]() .
.
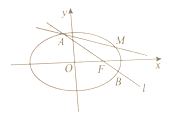
��������Բ![]() �ı����̣�
�ı����̣�
������ͼ����![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() Ϊ��
��![]() ����
����![]() ��ĶԳƵ�.
��ĶԳƵ�.
��1����֤��![]() ��
��
��2�����ʹ�![]() ��
��![]() ��ֱ���Ƿ�����㣿���ǣ�������ö��㣻�����ǣ���˵������.
��ֱ���Ƿ�����㣿���ǣ�������ö��㣻�����ǣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() .
.
��1������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��2������![]() �ĵ������䣻
�ĵ������䣻
��3�� ��֤����![]() ʱ��
ʱ��![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ����������������ȷ�ĸ����ǣ� ��
����������������ȷ�ĸ����ǣ� ��
�ٵ�![]() ʱ������
ʱ������![]() ��
��![]() ������Сֵ���ڵ�
������Сֵ���ڵ�![]() ʱ������
ʱ������![]() ��
��![]() �ǵ���������������
�ǵ���������������![]() ����
����![]() ���ܷ���
���ܷ���![]() ����������ʵ����.
����������ʵ����.
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪�� ��
��![]() ������������
������������ ��
��![]() Ϊ��������������ԭ��Ϊ���㣬
Ϊ��������������ԭ��Ϊ���㣬 ![]() ���������Ϊ���Ὠ��ֱ������ϵ.
���������Ϊ���Ὠ��ֱ������ϵ.
��1��������![]() �ļ����귽�̣�ֱ��
�ļ����귽�̣�ֱ��![]() ����ͨ���̣�
����ͨ���̣�
��2����ֱ��![]() ����ƽ��һ����λ�õ�ֱ��
����ƽ��һ����λ�õ�ֱ��![]() ����
����![]() ������
������![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ��
�� ![]() ��
�� ![]() ����
Ϊ����![]() ������һ�㣬��
������һ�㣬��![]() ��������ֵ.
��������ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com