
【题目】如图,四棱锥P﹣ABCD的底面ABCD为直角梯形,BC//AD,且AD=2AB=2BC=2,∠BAD=90°,△PAD为等边三角形,平面ABCD⊥平面PAD;点E、M分别为PD、PC的中点.
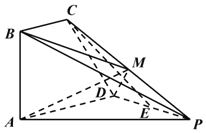
(1)证明:CE//平面PAB;
(2)求三棱锥M﹣BAD的体积;
(3)求直线DM与平面ABM所成角的正弦值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,利用三角形的中位线证得
,利用三角形的中位线证得![]() ,而
,而![]() ,由此证得
,由此证得![]() ,由此证得四边形
,由此证得四边形![]() 是平行四边形,进而证得
是平行四边形,进而证得![]() ,从而证得
,从而证得![]() 平面
平面![]() .
.
(2)根据等边三角形的性质,结合面面垂直的性质定理,求得![]() 到平面
到平面![]() 的距离,而
的距离,而![]() 是
是![]() 的中点,故
的中点,故![]() 到平面
到平面![]() 的距离是
的距离是![]() 到平面
到平面![]() 的距离的一半.由此求得
的距离的一半.由此求得![]() 到平面
到平面![]() 的距离,进而求得三棱锥
的距离,进而求得三棱锥![]() 的体积.
的体积.
(3)建立空间直角坐标系,利用直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量,计算出线面角的正弦值.
的法向量,计算出线面角的正弦值.
(1)证明:设PA的中点为N,连结EN,BN,
∵E为PD中点,∴EN为△PAD的中位线,
∴EN//AD,且EN![]() AD,
AD,
在梯形ABCD中,BC//AD,且BC![]() AD,
AD,
∴BC//EN,且BC=EN,∴四边形ENBC是平行四边形,∴CE//BN,
∵BN平面PAB,CE平面PAB,∴CE//平面PAB.
(2)解:∵四棱锥P﹣ABCD的底面ABCD为直角梯形,BC∥AD,且AD=2AB=2BC=2,∠BAD=90°,
∴![]() 1,
1,
∵△PAD为等边三角形,平面ABCD⊥平面PAD,点M是PC的中点.
设AD的中点为O,则PA=PD,∴PO⊥AD,
∴M到平面ABD的距离d![]() ,
,
∴三棱锥M﹣BAD的体积V![]() .
.
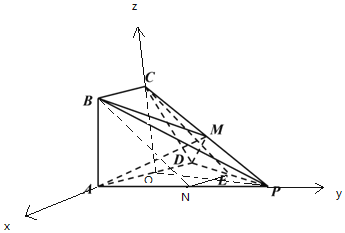
(3)∵平面PAD⊥平面ABCD,交线为AD,PO平面PAD,
∴PO⊥平面ABCD,
又∵CO//BA,∠BAD=90°,∴CO⊥AD,
∴OA,OC,OP,OC两两垂直,
以O为原点,OA,OC,OP,OC所在直线分别为x,y,z轴,建立空间直角坐标系,
则A(1,0,0),B(1,0,1),M(0,![]() ,
,![]() ),D(﹣1,0,0),
),D(﹣1,0,0),
![]() (0,0,1),
(0,0,1),![]() (﹣1,
(﹣1,![]() ,
,![]() ),
),
设平面ABM的法向量![]() (x,y,z),
(x,y,z),
则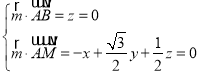 ,取x
,取x![]() ,得
,得![]() (
(![]() ),
),![]() (1,
(1,![]() ,
,![]() ),
),
cos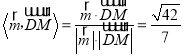 ,
,
∴直线DM与平面ABM所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 上至少存在两个不同的
上至少存在两个不同的![]() ,
,![]() 满足
满足![]() ,且函数
,且函数![]() 在
在![]() 上具有单调性,
上具有单调性,![]() 和
和![]() 分别为函数
分别为函数![]() 图象的一个对称中心和一条对称轴,则下列命题中正确的是( )
图象的一个对称中心和一条对称轴,则下列命题中正确的是( )
A.函数![]() 图象的两条相邻对称轴之间的距离为
图象的两条相邻对称轴之间的距离为![]()
B.函数![]() 图象关于直线
图象关于直线![]() 对称
对称
C.函数![]() 图象关于点
图象关于点![]() 对称
对称
D.函数![]() 在
在![]() 上是单调递减函数
上是单调递减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】造纸术是我国古代四大发明之一.纸张的规格是指纸张制成后,经过修整切边,裁成一定的尺寸.现在我国采用国际标准,规定以![]() 、
、![]() 、…、
、…、![]() ;
;![]() 、
、![]() 、…、
、…、![]() 等标记来表示纸张的幅面规格.复印纸幅面规格只采用
等标记来表示纸张的幅面规格.复印纸幅面规格只采用![]() 系列和
系列和![]() 系列,其中
系列,其中![]() 系列的幅面规格为:①
系列的幅面规格为:①![]() 规格的纸张的幅宽(以
规格的纸张的幅宽(以![]() 表示)和长度(以
表示)和长度(以![]() 表示)的比例关系为
表示)的比例关系为![]() ;②将
;②将![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格.
规格.![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格,…,如此对开至
规格,…,如此对开至![]() 规格.现有
规格.现有![]() 、
、![]() 、
、![]() 、…、
、…、![]() 纸各一张.若
纸各一张.若![]() 纸的面积为
纸的面积为![]() ,则这9张纸的面积之和等于______
,则这9张纸的面积之和等于______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是两条异面直线,直线
是两条异面直线,直线![]() 与
与![]() 都垂直,则下列说法正确的是( )
都垂直,则下列说法正确的是( )
A. 若![]() 平面
平面![]() ,则
,则![]()
B. 若![]() 平面
平面![]() ,则
,则![]() ,
,![]()
C. 存在平面![]() ,使得
,使得![]() ,
,![]() ,
,![]()
D. 存在平面![]() ,使得
,使得![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱柱![]() 的主视图和俯视图如图所示(图中一格为单位正方形),D、D1分别为棱AC和A1C1的中点.
的主视图和俯视图如图所示(图中一格为单位正方形),D、D1分别为棱AC和A1C1的中点.
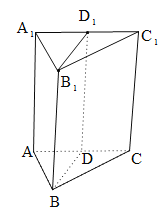
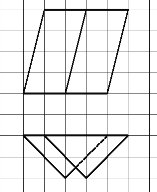
(1)求侧(左)视图的面积,并证明平面A1ACC1⊥平面B1BDD1
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面坐标系中xOy中,已知直线l的参数方程为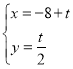 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为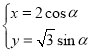 (
(![]() 为参数).以O为极点,x轴的非负半轴为极轴,建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴,建立极坐标系.
(1)求曲线C的普通方程和直线l的极坐标方程;
(2)设P为曲线C上的动点,求点P到直线l的距离的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com