
ЁОЬтФПЁПдьжНЪѕЪЧЮвЙњЙХДњЫФДѓЗЂУїжЎвЛ.жНеХЕФЙцИёЪЧжИжНеХжЦГЩКѓЃЌОЙ§аоећЧаБпЃЌВУГЩвЛЖЈЕФГпДч.ЯждкЮвЙњВЩгУЙњМЪБъзМЃЌЙцЖЈвд![]() ЁЂ
ЁЂ![]() ЁЂЁЁЂ
ЁЂЁЁЂ![]() ЃЛ
ЃЛ![]() ЁЂ
ЁЂ![]() ЁЂЁЁЂ
ЁЂЁЁЂ![]() ЕШБъМЧРДБэЪОжНеХЕФЗљУцЙцИё.ИДгЁжНЗљУцЙцИёжЛВЩгУ
ЕШБъМЧРДБэЪОжНеХЕФЗљУцЙцИё.ИДгЁжНЗљУцЙцИёжЛВЩгУ![]() ЯЕСаКЭ
ЯЕСаКЭ![]() ЯЕСаЃЌЦфжа
ЯЕСаЃЌЦфжа![]() ЯЕСаЕФЗљУцЙцИёЮЊЃКЂй
ЯЕСаЕФЗљУцЙцИёЮЊЃКЂй![]() ЙцИёЕФжНеХЕФЗљПэЃЈвд
ЙцИёЕФжНеХЕФЗљПэЃЈвд![]() БэЪОЃЉКЭГЄЖШЃЈвд
БэЪОЃЉКЭГЄЖШЃЈвд![]() БэЪОЃЉЕФБШР§ЙиЯЕЮЊ
БэЪОЃЉЕФБШР§ЙиЯЕЮЊ![]() ЃЛЂкНЋ
ЃЛЂкНЋ![]() жНеХбиГЄЖШЗНЯђЖдПЊГЩСНЕШЗжЃЌБуГЩЮЊ
жНеХбиГЄЖШЗНЯђЖдПЊГЩСНЕШЗжЃЌБуГЩЮЊ![]() ЙцИё.
ЙцИё.![]() жНеХбиГЄЖШЗНЯђЖдПЊГЩСНЕШЗжЃЌБуГЩЮЊ
жНеХбиГЄЖШЗНЯђЖдПЊГЩСНЕШЗжЃЌБуГЩЮЊ![]() ЙцИёЃЌЁЃЌШчДЫЖдПЊжС
ЙцИёЃЌЁЃЌШчДЫЖдПЊжС![]() ЙцИё.Яжга
ЙцИё.Яжга![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂЁЁЂ
ЁЂЁЁЂ![]() жНИївЛеХ.Шє
жНИївЛеХ.Шє![]() жНЕФУцЛ§ЮЊ
жНЕФУцЛ§ЮЊ![]() ЃЌдђет9еХжНЕФУцЛ§жЎКЭЕШгк______
ЃЌдђет9еХжНЕФУцЛ§жЎКЭЕШгк______![]() .
.

| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЃК
ЃК![]() ЕФзѓЁЂгвНЙЕуЗжБ№ЮЊ
ЕФзѓЁЂгвНЙЕуЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌШєЭждВОЙ§Еу
ЃЌШєЭждВОЙ§Еу![]() ЃЌЧвЁїPF1F2ЕФУцЛ§ЮЊ2ЃЎ
ЃЌЧвЁїPF1F2ЕФУцЛ§ЮЊ2ЃЎ
ЃЈ1ЃЉЧѓЭждВ![]() ЕФБъзМЗНГЬЃЛ
ЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉЩшаБТЪЮЊ1ЕФжБЯп![]() гывддЕуЮЊдВаФЃЌАыОЖЮЊ
гывддЕуЮЊдВаФЃЌАыОЖЮЊ![]() ЕФдВНЛгкAЃЌBСНЕуЃЌгыЭждВCНЛгкCЃЌDСНЕуЃЌЧв
ЕФдВНЛгкAЃЌBСНЕуЃЌгыЭждВCНЛгкCЃЌDСНЕуЃЌЧв![]() ЃЈ
ЃЈ![]() ЃЉЃЌЕБ
ЃЉЃЌЕБ![]() ШЁЕУзюаЁжЕЪБЃЌЧѓжБЯп
ШЁЕУзюаЁжЕЪБЃЌЧѓжБЯп![]() ЕФЗНГЬ.
ЕФЗНГЬ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛФъжЎМЦдкгкДКЃЌвЛШежЎМЦдкгкГПЃЌДКЬьЪЧВЅжжЕФМОНкЃЌЪЧЯЃЭћЕФПЊЖЫ.ФГжжжВЛЇЖдвЛПщЕиЕФ![]() ИіПгНјааВЅжжЃЌУПИіПгВЅ3СЃжжзгЃЌУПСЃжжзгЗЂбПЕФИХТЪОљЮЊ
ИіПгНјааВЅжжЃЌУПИіПгВЅ3СЃжжзгЃЌУПСЃжжзгЗЂбПЕФИХТЪОљЮЊ![]() ЃЌЧвУПСЃжжзгЪЧЗёЗЂбПЯрЛЅЖРСЂ.ЖдУПвЛИіПгЖјбдЃЌШчЙћжСЩйгаСНСЃжжзгЗЂбПЃЌдђВЛашвЊНјааВЙВЅжжЃЌЗёдђвЊВЙВЅжж.
ЃЌЧвУПСЃжжзгЪЧЗёЗЂбПЯрЛЅЖРСЂ.ЖдУПвЛИіПгЖјбдЃЌШчЙћжСЩйгаСНСЃжжзгЗЂбПЃЌдђВЛашвЊНјааВЙВЅжжЃЌЗёдђвЊВЙВЅжж.
ЃЈ1ЃЉЕБ![]() ШЁКЮжЕЪБЃЌга3ИіПгвЊВЙВЅжжЕФИХТЪзюДѓЃПзюДѓИХТЪЮЊЖрЩйЃП
ШЁКЮжЕЪБЃЌга3ИіПгвЊВЙВЅжжЕФИХТЪзюДѓЃПзюДѓИХТЪЮЊЖрЩйЃП
ЃЈ2ЃЉЕБ![]() ЪБЃЌгУ
ЪБЃЌгУ![]() БэЪОвЊВЙВЅжжЕФПгЕФИіЪ§ЃЌЧѓ
БэЪОвЊВЙВЅжжЕФПгЕФИіЪ§ЃЌЧѓ![]() ЕФЗжВМСагыЪ§бЇЦкЭћ.
ЕФЗжВМСагыЪ§бЇЦкЭћ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊfЃЈxЃЉЃНЉx+|2x+1|ЃЌВЛЕШЪНfЃЈxЃЉЃМ2ЕФНтМЏЪЧMЃЎ
ЃЈЂёЃЉЧѓМЏКЯMЃЛ
ЃЈЂђЃЉЩшaЃЌbЁЪMЃЌжЄУїЃК|ab|+1ЃО|a|+|b|ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЙигке§ЗНЬх![]() ЃЌгаЯТСаЫФИіУќЬтЃК
ЃЌгаЯТСаЫФИіУќЬтЃК
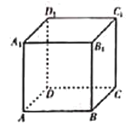
Ђй![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЮЊ45ЁуЃЛ
ЫљГЩНЧЮЊ45ЁуЃЛ
ЂкШ§РтзЖ![]() гыШ§РтзЖ
гыШ§РтзЖ![]() ЕФЬхЛ§БШЮЊ
ЕФЬхЛ§БШЮЊ![]() ЃЛ
ЃЛ
ЂлДцдкЮЈвЛЦНУц![]() .ЪЙ
.ЪЙ![]() ЦНУц
ЦНУц![]() Чв
Чв![]() НиДЫе§ЗНЬхЫљЕУНиУцЮЊе§СљБпаЮЃЛ
НиДЫе§ЗНЬхЫљЕУНиУцЮЊе§СљБпаЮЃЛ
ЂмЙ§![]() зїЦНУц
зїЦНУц![]() ЃЌЪЙЕУРт
ЃЌЪЙЕУРт![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ![]() дкЦНУц
дкЦНУц![]() ЩЯЕФе§ЭЖгАЕФГЄЖШЯрЕШ.дђетбљЕФЦНУц
ЩЯЕФе§ЭЖгАЕФГЄЖШЯрЕШ.дђетбљЕФЦНУц![]() гаЧвНігавЛИі.
гаЧвНігавЛИі.
ЩЯЪіЫФИіУќЬтжаЃЌе§ШЗУќЬтЕФађКХЮЊ________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕу![]() гыЖЈЕу
гыЖЈЕу![]() ЕФОрРыКЭЫќЕНжБЯп
ЕФОрРыКЭЫќЕНжБЯп![]() ЕФОрРыЕФБШЪЧГЃЪ§
ЕФОрРыЕФБШЪЧГЃЪ§![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЕФЙьМЃЮЊЧњЯп
ЕФЙьМЃЮЊЧњЯп![]() .
.
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() гыЧњЯп
гыЧњЯп![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЩш
СНЕуЃЌЩш![]() ЕФжаЕуЮЊ
ЕФжаЕуЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() СНЕуЮЊЧњЯп
СНЕуЮЊЧњЯп![]() ЩЯЙигкдЕу
ЩЯЙигкдЕу![]() ЖдГЦЕФСНЕуЃЌЧв
ЖдГЦЕФСНЕуЃЌЧв![]() ЃЈ
ЃЈ![]() ЃЉЃЌЧѓЫФБпаЮ
ЃЉЃЌЧѓЫФБпаЮ![]() УцЛ§ЕФШЁжЕЗЖЮЇ.
УцЛ§ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() НЛгкВЛЭЌЕФСНЕу
НЛгкВЛЭЌЕФСНЕу![]() ЃЌ
ЃЌ![]() ЮЊХзЮяЯп
ЮЊХзЮяЯп![]() ЕФНЙЕуЃЌ
ЕФНЙЕуЃЌ![]() ЮЊзјБъдЕуЃЌ
ЮЊзјБъдЕуЃЌ![]() ЪЧ
ЪЧ![]() ЕФжиаФЃЌжБЯп
ЕФжиаФЃЌжБЯп![]() КуЙ§Еу
КуЙ§Еу![]() .
.
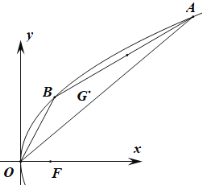
ЃЈ1ЃЉШє![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() аБТЪЕФШЁжЕЗЖЮЇЃЛ
аБТЪЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШє![]() ЪЧАыЭждВ
ЪЧАыЭждВ![]() ЩЯЕФЖЏЕуЃЌжБЯп
ЩЯЕФЖЏЕуЃЌжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() НЛгкВЛЭЌЕФСНЕу
НЛгкВЛЭЌЕФСНЕу![]() ЃЌ
ЃЌ![]() .ЕБ
.ЕБ![]() ЪБЃЌЧѓЁї
ЪБЃЌЧѓЁї![]() УцЛ§ЕФШЁжЕЗЖЮЇ.
УцЛ§ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФРтзЖPЉABCDЕФЕзУцABCDЮЊжБНЧЬнаЮЃЌBC//ADЃЌЧвAD=2AB=2BC=2ЃЌЁЯBAD=90ЁуЃЌЁїPADЮЊЕШБпШ§НЧаЮЃЌЦНУцABCDЁЭЦНУцPADЃЛЕуEЁЂMЗжБ№ЮЊPDЁЂPCЕФжаЕу.
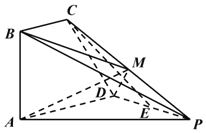
ЃЈ1ЃЉжЄУїЃКCE//ЦНУцPABЃЛ
ЃЈ2ЃЉЧѓШ§РтзЖMЉBADЕФЬхЛ§ЃЛ
ЃЈ3ЃЉЧѓжБЯпDMгыЦНУцABMЫљГЩНЧЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
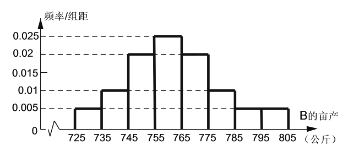
ЁОЬтФПЁПФГЕижжжВГЃЙцЕОAКЭдгНЛЕОBЃЌГЃЙцЕОAЕФФЖВњЮШЖЈЮЊ500ЙЋНяЃЌНёФъЕЅМлЮЊ3.50дЊЃЏЙЋНяЃЌЙРМЦУїФъЕЅМлВЛБфЕФПЩФмадЮЊ10%ЃЌБфЮЊ3.60дЊЃЏЙЋНяЕФПЩФмадЮЊ60%ЃЌБфЮЊ3.70дЊЃЏЙЋНяЕФПЩФмадЮЊ30%ЃЎЭГМЦдгНЛЕОBЕФФЖВњЪ§ОнЃЌЕУЕНФЖВњЕФЦЕТЪЗжВМжБЗНЭМШчЯТЃЛЭГМЦНќ10ФъРДдгНЛЕОBЕФЕЅМлЃЈЕЅЮЛЃКдЊ/ЙЋНяЃЉгыжжжВФЖЪ§ЃЈЕЅЮЛЃКЭђФЖЃЉЕФЙиЯЕЃЌЕУЕНЕФ10зщЪ§ОнМЧЮЊ![]() ЃЌВЂЕУЕНЩЂЕуЭМШчЯТЃЌВЮПМЪ§ОнМћЯТЃЎ
ЃЌВЂЕУЕНЩЂЕуЭМШчЯТЃЌВЮПМЪ§ОнМћЯТЃЎ
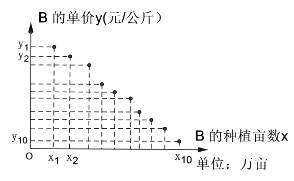
ЃЈ1ЃЉЙРМЦУїФъГЃЙцЕОAЕФЕЅМлЦНОљжЕЃЛ
ЃЈ2ЃЉдкЦЕТЪЗжВМжБЗНЭМжаЃЌИїзщЕФШЁжЕАДжаМфжЕРДМЦЫуЃЌЧѓдгНЛЕОBЕФФЖВњЦНОљжЕЃЛвдЦЕТЪзїЮЊИХТЪЃЌдЄМЦНЋРДШ§ФъжажСЩйгаЖўФъЃЌдгНЛЕОBЕФФЖВњГЌЙ§765ЙЋНяЕФИХТЪЃЛ
ЃЈ3ЃЉХаЖЯдгНЛЕОBЕФЕЅМлyЃЈЕЅЮЛЃКдЊ/ЙЋНяЃЉгыжжжВФЖЪ§xЃЈЕЅЮЛЃКЭђФЖЃЉЪЧЗёЯпадЯрЙиЃПШєЯрЙиЃЌЪдИљОнвдЯТЕФВЮПМЪ§ОнЧѓГіyЙигкxЕФЯпадЛиЙщЗНГЬЃЛЕїВщЕУжЊУїФъДЫЕидгНЛЕОBЕФжжжВФЖЪ§дЄМЦЮЊ2ЭђФЖЃЎШєдкГЃЙцЕОAКЭдгНЛЕОBжабЁдёЃЌУїФъжжжВФФжжЫЎЕОЪеШыИќИпЃП
ЭГМЦВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ИНЃКЯпадЛиЙщЗНГЬ![]() ЃЌ
ЃЌ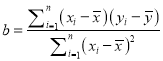 ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com