
【题目】如图所示,在多面体![]() 中,
中, ![]() 与
与![]() 均为边长为2的正方形,
均为边长为2的正方形, ![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,且平面
,且平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.

【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)由线面垂直可得![]() ,由
,由![]() 为等腰直角三角形可得
为等腰直角三角形可得![]() ,从而
,从而![]() 平面
平面![]() ,进而可得平面
,进而可得平面![]() 平面
平面![]() ;(Ⅱ)以
;(Ⅱ)以![]() 为原点,以
为原点,以![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立如图所示的空间直角坐标系,分别求出平面
轴建立如图所示的空间直角坐标系,分别求出平面![]() 与平面
与平面![]() 的的一个法向量,根据空间向量夹角余弦公式,可得结果
的的一个法向量,根据空间向量夹角余弦公式,可得结果
试题解析:(Ⅰ) ![]() 平面
平面![]() 平面
平面![]() ,且
,且![]() ,
,
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
, ![]() .
.
又![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,
, ![]() .
.
![]() ,
, ![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ)![]() 平面
平面![]() 平面
平面![]() ,
, ![]() ,
,
![]() 平面
平面![]() ,
,
![]() ,
, ![]() .
.
又![]() ,
, ![]() 以
以![]() 为原点,以
为原点,以![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立如图所示的空间直角坐标系,则由题意,知
轴建立如图所示的空间直角坐标系,则由题意,知![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则
由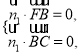 得
得![]() 取
取![]() ,则
,则![]() .
.
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则
由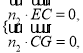 得
得![]() 取
取![]() ,则
,则![]() ,
,
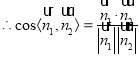
![]() .
.
![]() 平面
平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.
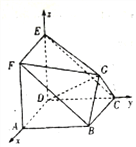
【方法点晴】本题主要考查线面垂直的性质、面面垂直的判定,利用空间向量二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


科目:高中数学 来源: 题型:
【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要付出设备的维修和工人工资等费用an的信息如图. 
(1)求an;
(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(I)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(II)求证:![]() 平面
平面![]() ;
;
(II)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一壁画,最高点A处离地面AO=4m,最低点B处离地面BO=2m,观赏它的C点在过墙角O点与地面成30°角的射线上. 
(1)设点C到墙的距离为x,当x= ![]() m时,求tanθ的值;
m时,求tanθ的值;
(2)问C点离墙多远时,视角θ最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥CD,∠ABC=90°,且CD=2,AB=BC=PA=1,PD= ![]() .
. 
(1)求三棱锥A﹣PCD的体积;
(2)问:棱PB上是否存在点E,使得PD∥平面ACE?若存在,求出 ![]() 的值,并加以证明;若不存在,请说明理由.
的值,并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个几何体的三视图如图所示. 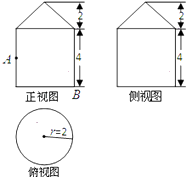
(1)求此几何体的表面积;
(2)在如图的正视图中,如果点A为所在线段中点,点B为顶点,求在几何体侧面上从点A到点B的最短路径的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个无穷数列![]() 和
和![]() 的前
的前![]() 项和分别为
项和分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,对任意的
,对任意的![]() ,都有
,都有![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() 为等差数列,对任意的
为等差数列,对任意的![]() ,都有
,都有![]() .证明:
.证明: ![]() ;
;
(3)若![]() 为等比数列,
为等比数列, ![]() ,
, ![]() ,求满足
,求满足![]()
![]() 的
的![]() 值.
值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com