
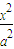 +
+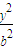 =1(a>b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为b2
=1(a>b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为b2 ,类比,P是双曲线
,类比,P是双曲线 -
-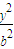 =1(a>0,b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为 .
=1(a>0,b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为 . 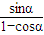 .设|PF1|=r1,|PF2|=r2,根据三角形面积公式可表示出△PF1F2的面积,由余弦定理可求得r1r2的表达式,进而求得S与b和tanθ的关系式,原式得证.
.设|PF1|=r1,|PF2|=r2,根据三角形面积公式可表示出△PF1F2的面积,由余弦定理可求得r1r2的表达式,进而求得S与b和tanθ的关系式,原式得证.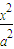 -
-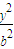 =1(a>0,b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为 b2
=1(a>0,b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为 b2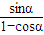 .
. r1r2sin2θ,又|F1F2|=2c,
r1r2sin2θ,又|F1F2|=2c,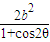 .
. •
•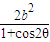 sin2θ=b2
sin2θ=b2 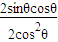 =b2
=b2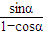 .
.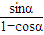 .
. r1r2sin2θ.若能消去r1r2,问题即获解决.
r1r2sin2θ.若能消去r1r2,问题即获解决. 

 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| sinα |
| 1+cosα |
| x2 |
| a2 |
| y2 |
| b2 |
| sinα |
| 1-cosα |
| sinα |
| 1-cosα |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 +
+ =1(a>b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为b2
=1(a>b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为b2 ,类比,P是双曲线
,类比,P是双曲线 -
- =1(a>0,b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为________.
=1(a>0,b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com