
(Ⅰ)若b=2,且h(x)=f(x)-g(x)存在单调递减区间,求a的取值范围;
(Ⅱ)设函数f(x)的图象C1与函数g(x)图象C2交于点P、Q,过线段PQ的中点作x轴的垂线分别交C1,C2于点M、N,证明C1在点M处的切线与C2在点N处的切线不平行。
21.解:(I)![]() ,
,
则![]()
因为函数h(x)存在单调递减区间,所以![]() <0有解.
<0有解.
又因为x>0时,则ax2+2x-1>0有x>0的解.
①当a>0时,y=ax2+2x-1为开口向上的抛物线,ax2+2x-1>0总有x>0的解;
②当a<0时,y=ax2+2x-1为开口向下的抛物线,而ax2+2x-1>0有x>0的解;
则△=4+4a>0,且方程ax2+2x-1=0至少有一正根.此时,-1<a<0.
综上所述,a的取值范围为(-1,0)∪(0,+∞).
(II)证法一 设点P、Q的坐标分别是(x1, y1),(x2, y2),0<x1<x2.
则点M、N的横坐标为![]()
C1在点M处的切线斜率为![]()
C2在点N处的切线斜率为![]()
假设C1在点M处的切线与C2在点N处的切线平行,则k1=k2.
即![]() ,则
,则
![]() =
=![]()
所以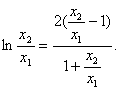
设![]() 则
则![]() ①
①
令![]()
则![]()
因为![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() )上单调递增. 故
)上单调递增. 故![]()
则![]() . 这与①矛盾,假设不成立.
. 这与①矛盾,假设不成立.
故C1在点M处的切线与C2在点N处的切线不平行.
证法二:同证法一得![]()
因为![]() ,所以
,所以![]()
令![]() ,得
,得![]() ②
②
令![]()
因为![]() ,所以
,所以![]() 时,
时,![]()
故![]() 在[1,+
在[1,+![]() 上单调递增.从而
上单调递增.从而![]() ,即
,即![]()
于是![]() 在[1,+
在[1,+![]() 上单调递增.
上单调递增.
故![]() 即
即![]() 这与②矛盾,假设不成立.
这与②矛盾,假设不成立.
故C1在点M处的切线与C2在点N处的切线不平行.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知函数f(x)=ax2-2x+1,g(x)=ln(x+1).
(1)求函数y=g(x)-x在[0,1]上的最小值;
(2)当a≥![]() 时,函数t(x)=f(x)+g(x)的图像记为曲线C,曲线C在点(0,1)处的切线为l,是否存在a使l与曲线C有且仅有一个公共点?若存在,求出所有a的值;否则,说明理由.
时,函数t(x)=f(x)+g(x)的图像记为曲线C,曲线C在点(0,1)处的切线为l,是否存在a使l与曲线C有且仅有一个公共点?若存在,求出所有a的值;否则,说明理由.
(3)当x≥0时,g(x)≥-![]() f(x)+
f(x)+![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届湖北省大治二中高二3月联考文科数学试卷(解析版) 题型:解答题
已知函数f(x)=x3+x-16,
(1)求曲线y=f(x)在点(2,-6)处的切线的方程;
(2)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程及切点坐标;
查看答案和解析>>
科目:高中数学 来源:2012年陕西省高二下期第一次月考理科数学试卷(解析版) 题型:解答题
已知函数f(x)=x3-3x及y=f(x)上一点P(1,-2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于P的直线方程.
查看答案和解析>>
科目:高中数学 来源:新课标高三数学导数专项训练(河北) 题型:解答题
已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在x=1处的切线为l:3x-y+1=0,当x=时,y=f(x)有极值.
(1)求a、b、c的值;
(2)求y=f(x)在[-3,1]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:新课标高三数学导数专项训练(河北) 题型:解答题
已知函数f(x)=x3-2x2+ax(x∈R,a∈R),在曲线y=f(x)的所有切线中,有且仅有一条切线l与直线y=x垂直.
(1)求a的值和切线l的方程;
(2)设曲线y=f(x)上任一点处的切线的倾斜角为θ,求θ的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com