
【题目】在![]() 中,角
中,角![]() 的三条对边分别为
的三条对边分别为![]() ,
,![]() .
.
(1)求![]() ;
;
(2)点![]() 在边
在边![]() 上,
上,![]() ,
,![]() ,
,![]() ,求
,求![]() .
.
【答案】(1)![]() ;(2)2
;(2)2
【解析】
(1)由题意利用正弦定理与三角恒等变换求出sinB与cosB的关系,得出tanB的值,从而求出B的值;
(2)根据互补的两角正弦值相等,得到sin∠ADB=sin∠ADC的值,再利用正弦、余弦定理求得AD、AC的值.
(1)由bcosC![]() bsinC=a,
bsinC=a,
利用正弦定理得:sinBcosC![]() sinBsinC=sinA,
sinBsinC=sinA,
即sinBcosC![]() sinBsinC=sinBcosC+cosBsinC,
sinBsinC=sinBcosC+cosBsinC,
得![]() sinBsinC=cosBsinC,
sinBsinC=cosBsinC,
又C∈(0,π),所以sinC≠0,
所以![]() sinB=cosB,
sinB=cosB,
得tanB![]() ,
,
又B∈(0,π),所以B![]() ;
;
(2)如图所示,
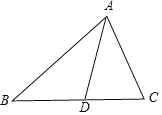
由cos∠ADC![]() ,∠ADC∈(0,π),
,∠ADC∈(0,π),
所以sin∠ADC![]() ,
,
由因为∠ADB=π﹣∠ADC,
所以sin∠ADB=sin∠ADC![]() ;
;
在△ABD中,由正弦定理得,![]() ,
,
且AB=4,B![]() ,
,
所以AD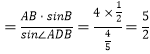 ;
;
在△ACD中,由余弦定理得,
AC2=AD2+DC2﹣2ADDCcos∠ADC
![]() 2
2![]() 4,
4,
解得AC=2.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
【题目】已知两个不相等的非零向量 ![]() ,
, ![]() ,两组向量
,两组向量 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 和
和 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 均由2个
均由2个 ![]() 和3个
和3个 ![]() 排列而成,记S=
排列而成,记S= ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() ,Smin表示S所有可能取值中的最小值.则下列命题正确的是(写出所有正确命题的编号).
,Smin表示S所有可能取值中的最小值.则下列命题正确的是(写出所有正确命题的编号).
①S有5个不同的值;
②若 ![]() ⊥
⊥ ![]() ,则Smin与|
,则Smin与| |无关;
③若 ![]() ∥
∥ ![]() ,则Smin与|
,则Smin与| ![]() |无关;
|无关;
④若| ![]() |>4|
|>4| ![]() |,则Smin>0;
|,则Smin>0;
⑤若| ![]() |=2|
|=2| ![]() |,Smin=8|
|,Smin=8| ![]() |2 , 则
|2 , 则 ![]() 与
与 ![]() 的夹角为
的夹角为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,过A1、C、D三点的平面记为α,BB1与α的交点为Q. 
(1)证明:Q为BB1的中点;
(2)求此四棱柱被平面α所分成上下两部分的体积之比;
(3)若AA1=4,CD=2,梯形ABCD的面积为6,求平面α与底面ABCD所成二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关线性回归分析的四个命题:
①线性回归直线必过样本数据的中心点(![]() );
);
②回归直线就是散点图中经过样本数据点最多的那条直线;
③当相关性系数![]() 时,两个变量正相关;
时,两个变量正相关;
④如果两个变量的相关性越强,则相关性系数![]() 就越接近于
就越接近于![]() .
.
其中真命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别是a,b,c,且a2+b2+ ![]() ab=c2 .
ab=c2 .
(1)求C;
(2)设cosAcosB= ![]() ,
, ![]() =
= ![]() ,求tanα的值.
,求tanα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图F1、F2是椭圆C1: ![]() +y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
+y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,且当x<0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象如图所示,

(1)画出函数f(x),x∈R剩余部分的图象,并根据图象写出函数f(x),x∈R的单调区间;(只写答案)
(2)求函数f(x),x∈R的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com