
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且2asin A=(2b+c)sin B+(2c+b)sin C.
(1)求A的大小; (2)若sin B+sin C=1,试判断△ABC的形状.(12分)
【答案】(1)A=120°.(2)B=C=30°.
【解析】
(1)利用正弦定理,余弦定理即可求![]() 的大小;
的大小;
方法一 由(1)得sin2A=sin2B+sin2C+sin Bsin C,
又A=120°,∴sin2B+sin2C+sin Bsin C=![]() ,
,
∵sin B+sin C=1,∴sin C=1-sin B.,代入求出![]() ,即可判断;
,即可判断;
方法二 由(1)A=120°,∴B+C=60°,
则C=60°-B,∴sin B+sin C=sin(B+60°)=1,求出![]() ,即可判断;
,即可判断;
解 (1)由已知,根据正弦定理得2a2=(2b+c)b+(2c+b)c,
即a2=b2+c2+bc.
由余弦定理得a2=b2+c2-2bccos A,
故cos A=-![]() ,A=120°.
,A=120°.
(2)方法一 由(1)得sin2A=sin2B+sin2C+sin Bsin C,
又A=120°,∴sin2B+sin2C+sin Bsin C=![]() ,
,
∵sin B+sin C=1,∴sin C=1-sin B.
∴sin2B+(1-sin B)2+sin B(1-sin B)=![]() ,
,
即sin2B-sin B+![]() =0.
=0.
解得sin B=![]() .故sin C=
.故sin C=![]() .
.
∴B=C=30°.
所以,△ABC是等腰的钝角三角形.
方法二 由(1)A=120°,∴B+C=60°,
则C=60°-B,
∴sin B+sin C=sin B+sin(60°-B)=sin B+![]() cos B-
cos B-![]() sin B
sin B
=![]() sin B+
sin B+![]() cos B=sin(B+60°)=1,
cos B=sin(B+60°)=1,
∴B=30°,C=30°.
∴△ABC是等腰的钝角三角形.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】若将函数y=2sin 2x的图像向左平移 ![]() 个单位长度,则评议后图象的对称轴为( )
个单位长度,则评议后图象的对称轴为( )
A.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
B.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
C.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
D.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从含有两件正品a,b和一件次品c的3件产品中每次任取一件,连续取两次,求取出的两件产品中,恰有一件是次品的概率。
(1)每次取出不放回;(2)每次取出放回;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P﹣A1B1C1D1 , 下部的形状是正四棱柱ABCD﹣A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.
(1)若AB=6m,PO1=2m,则仓库的容积是多少?
(2)若正四棱柱的侧棱长为6m,则当PO1为多少时,仓库的容积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+bx(a>0,b>0,a≠1,b≠1).
(1)设a=2,b= ![]() .
.
①求方程f(x)=2的根;
②若对于任意x∈R,不等式f(2x)≥mf(x)﹣6恒成立,求实数m的最大值;
(2)若0<a<1,b>1,函数g(x)=f(x)﹣2有且只有1个零点,求ab的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列{bn}中的b3、b4、b5.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)数列{bn}的前n项和为Sn,求证:数列{Sn+![]() }是等比数列.
}是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察下列等式:
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2=
)﹣2= ![]() ×1×2;
×1×2;
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+sin(
)﹣2+sin( ![]() )﹣2=
)﹣2= ![]() ×2×3;
×2×3;
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+…+sin(
)﹣2+…+sin( ![]() )﹣2=
)﹣2= ![]() ×3×4;
×3×4;
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+…+sin(
)﹣2+…+sin( ![]() )﹣2=
)﹣2= ![]() ×4×5;
×4×5;
…
照此规律,
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+…+(sin
)﹣2+…+(sin ![]() )﹣2= .
)﹣2= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABC﹣DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.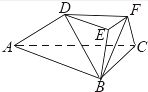
(1)求证:BF⊥平面ACFD;
(2)求直线BD与平面ACFD所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com