
【题目】【2016高考山东文数】已知椭圆C:![]() (a>b>0)的长轴长为4,焦距为2
(a>b>0)的长轴长为4,焦距为2![]() .
.
(I)求椭圆C的方程;
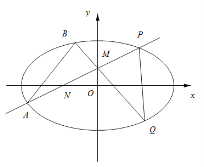
(Ⅱ)过动点M(0,m)(m>0)的直线交x轴与点N,交C于点A,P(P在第一象限),且M是线段PN的中点.过点P作x轴的垂线交C于另一点Q,延长线QM交C于点B.
(i)设直线PM、QM的斜率分别为k、k',证明![]() 为定值.
为定值.
(ii)求直线AB的斜率的最小值.
【答案】(Ⅰ) ![]() .(Ⅱ)(i)见解析;(ii)直线AB 的斜率的最小值为
.(Ⅱ)(i)见解析;(ii)直线AB 的斜率的最小值为![]() .
.
【解析】
试题分析:(Ⅰ)分别计算![]() 即得.
即得.
(Ⅱ)(i)设![]() ,
,
利用对称点可得![]()
得到直线PM的斜率,直线QM的斜率,即可证得.
(ii)设![]() ,分别将直线PA的方程
,分别将直线PA的方程![]() ,直线QB的方程
,直线QB的方程![]() 与椭圆方程
与椭圆方程
![]() 联立,
联立,
应用一元二次方程根与系数的关系得到![]() 、
、![]() 及
及![]() 用
用![]() 表示的式子,进一步应用基本不等式即得.
表示的式子,进一步应用基本不等式即得.
试题解析:(Ⅰ)设椭圆的半焦距为c,
由题意知![]() ,
,
所以![]() ,
,
所以椭圆C的方程为![]() .
.
(Ⅱ)(i)设![]() ,
,
由![]() ,可得
,可得![]()
所以 直线PM的斜率![]() ,
,
直线QM的斜率![]() .
.
此时![]() ,所以
,所以![]() 为定值
为定值![]() .
.
(ii)设![]() ,
,
直线PA的方程为![]() ,
,
直线QB的方程为![]() .
.
联立 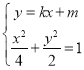 ,
,
整理得![]() .
.
由![]() 可得
可得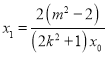 ,
,
所以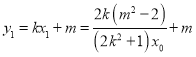 ,
,
同理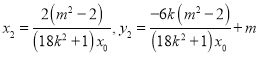 .
.
所以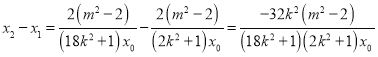 ,
,
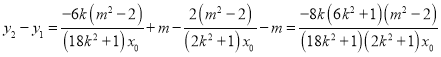 ,
,
所以![]()
由![]() ,可知
,可知![]() ,
,
所以![]() ,等号当且仅当
,等号当且仅当![]() 时取得.
时取得.
此时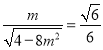 ,即
,即![]() ,符号题意.
,符号题意.
所以直线AB 的斜率的最小值为![]() .
.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
【题目】百子回归图是由1,2,3…,100无重复排列而成的正方形数表,它是一部数化的澳门简史,如:中央四位“19 99 12 20”标示澳门回归日期,最后一行中间两位“23 50”标示澳门面积,…,同时它也是十阶幻方,其每行10个数之和,每列10个数之和,每条对角线10个数之和均相等,则这个和为.
. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
在如图所示的多面体中,四边形![]() 和
和![]() 都为矩形。
都为矩形。

(Ⅰ)若![]() ,证明:直线
,证明:直线![]() 平面
平面![]() ;
;
(Ⅱ)设![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() 的中点,在线段
的中点,在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 平面
平面![]() ?请证明你的结论。
?请证明你的结论。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b﹣2c)cosA=a﹣2acos2 ![]() .
.
(1)求角A的值;
(2)若a= ![]() ,则求b+c的取值范围.
,则求b+c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(1+sin2x,sinx﹣cosx),
=(1+sin2x,sinx﹣cosx), ![]() =(1,sinx+cosx),函数f(x)=
=(1,sinx+cosx),函数f(x)= ![]()
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的最大值及取得最大值相应的x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究学生在考试时做解答题的情况,老师从甲、乙两个班级里各随机抽取了五份答卷并对解答题第16题(满分13分)的得分进行统计,得到对应的甲、乙两组数据,其茎叶图如图所示,其中x,y∈{0,1,2,3},已知甲组数据的中位数比乙组数据的平均数多 ![]() ,则x+y的值为( )
,则x+y的值为( ) 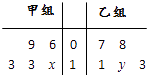
A.5
B.4
C.3
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点
的左、右焦点![]() ,
,![]() ,离心率
,离心率![]() ,短轴长为2.
,短轴长为2.
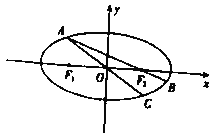
(Ⅰ)求椭圆的方程;
(Ⅱ)如图,点![]() 为椭圆上一动点(非长轴端点),
为椭圆上一动点(非长轴端点),![]() 的延长线于椭圆交于
的延长线于椭圆交于![]() 点,
点,![]() 的延长线于椭圆交于
的延长线于椭圆交于![]() 点,求
点,求![]() 面积的最大值
面积的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com