
已知,圆C: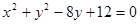 ,直线
,直线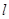 :
: .
.
(1) 当a为何值时,直线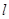 与圆C相切;
与圆C相切;
(2) 当直线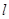 与圆C相交于A、B两点,且
与圆C相交于A、B两点,且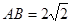 时,求直线
时,求直线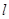 的方程.
的方程.
(1)  (2)
直线
(2)
直线 的方程是
的方程是 和
和
【解析】(1)根据圆心到直线的距离等于半径建立关于a的方程,求出a值.
(2)根据 ,借助弦长公式可求得圆心到直线的距离,从而利用点到直线的距离公式建立关于a的方程,求出a值.
,借助弦长公式可求得圆心到直线的距离,从而利用点到直线的距离公式建立关于a的方程,求出a值.
解:将圆C的方程 配方得标准方程为
配方得标准方程为 ,则此圆的圆心为(0 , 4),半径为2.
……………………………2分
,则此圆的圆心为(0 , 4),半径为2.
……………………………2分
(1) 若直线 与圆C相切,则有
与圆C相切,则有 . …………………………4分
. …………………………4分
解得 . ……………………6分
. ……………………6分
(2) 解法一:过圆心C作CD⊥AB, ………7分
则根据题意和圆的性质,得
 …………………10分
…………………10分
解得 .……………12分
.……………12分
(解法二:联立方程 并消去
并消去 ,得
,得
 .
.
设此方程的两根分别为 、
、 ,则用
,则用 即可求出a.)
即可求出a.)
∴直线 的方程是
的方程是 和
和 .…………………………14分
.…………………………14分


科目:高中数学 来源:2012-2013学年广东省雷州市高三第二次月考数学文试卷(解析版) 题型:解答题
(本小题满分14分)
已知,圆C: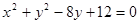 ,直线
,直线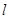 :
: .
.
(1) 当a为何值时,直线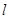 与圆C相切;
与圆C相切;
(2) 当直线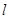 与圆C相交于A、B两点,且
与圆C相交于A、B两点,且 时,求直线
时,求直线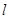 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省高二10月阶段性检测数学试卷(解析版) 题型:解答题
(本小题满分10分)已知,圆C: ,直线
,直线 :
: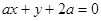 .
.
(1) 当a为何值时,直线 与圆C相切;
与圆C相切;
(2) 当直线 与圆C相交于A、B两点,且
与圆C相交于A、B两点,且 时,求直线
时,求直线 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com