
【题目】已知cos(75°+α)=![]() ,α是第三象限角,
,α是第三象限角,
(1)求sin(75°+α) 的值.
(2)求cos(α-15°) 的值.
(3)求sin(195°-α)+cos(105o-α)的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3) ![]() .
.
【解析】试题分析:(1)由![]() ,
, ![]() 是第三象限角,可得
是第三象限角,可得![]() 是第四象限角,根据同角三角函数之间的关系求解即可;(2)直接根据诱导公式可得结果;(3)根据诱导公式结合(2)的结论可得结果.
是第四象限角,根据同角三角函数之间的关系求解即可;(2)直接根据诱导公式可得结果;(3)根据诱导公式结合(2)的结论可得结果.
试题解析:(1)∵cos(75°+α)=![]() >0,α是第三象限角,
>0,α是第三象限角,
∴75°+α是第四象限角,
且sin(75°+α)=-![]() =-
=-![]() .
.
(2)cos(α-15°)= cos[90°-(75°+α)]= sin(75°+α)= -![]()
(3)∴sin(195°-α) +cos(105o-α)
=sin[180°+(15°-α)]+cos[180o o-(75°+α)]
=-sin(15°-α) -cos(75°+α)
=-sin[90°-(75°+α)] -cos(75°+α)
=-2cos(75°+α)=![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】为了预防甲型![]() 流感,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时室内每立方米空气中的含药量
流感,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时室内每立方米空气中的含药量![]() 与时间
与时间![]() 成正比例,药物燃烧完后满足
成正比例,药物燃烧完后满足![]() ,如图所示,现测得药物8
,如图所示,现测得药物8![]() 燃毕,此时室内空气中每立方米的含药量为6
燃毕,此时室内空气中每立方米的含药量为6![]() ,请按题中所供给的信息,解答下列各题.
,请按题中所供给的信息,解答下列各题.
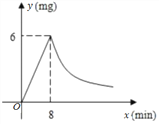
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)研究表明,当空气中每立方米的含药量不低于![]() 且持续时间不低于
且持续时间不低于![]() 时才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
时才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在半径为![]() 的半圆形(
的半圆形(![]() 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料![]() ,其中
,其中![]() 在直径上,点
在直径上,点![]() 在圆周上.
在圆周上.
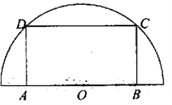
(1)设![]() ,将矩形
,将矩形![]() 的面积
的面积![]() 表示成
表示成![]() 的函数,并写出其定义域;
的函数,并写出其定义域;
(2)怎样截取,才能使矩形材料![]() 的面积最大?并求出最大面积.
的面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数h(x)=ax3+bx2+cx+d(a≠0)图象的对称中心为M(x0 , h(x0)),记函数h(x)的导函数为g(x),则有g′(x0)=0,设函数f(x)=x3﹣3x2+2,则f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(
)+f( ![]() )= .
)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1 , AB⊥AN,CB=BA=AN= ![]() BB1 .
BB1 . 
(1)求证:BN⊥平面C1B1N;
(2)求二面角C﹣C1N﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,an+1= ![]() (n∈N*).
(n∈N*).
(1)求证:{ ![]() +
+ ![]() }为等比数列,并求{an}的通项公式an;
}为等比数列,并求{an}的通项公式an;
(2)数列{bn}满足bn=(3n﹣1) ![]() an , 求数列{bn}的前n项和Tn .
an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业常年生产一种出口产品,根据预测可知,进入21世纪以来,该产品的产量平稳增长.记2009年为第1年,且前4年中,第![]() 年与年产量
年与年产量![]() 万件之间的关系如下表所示:
万件之间的关系如下表所示:

若![]() 近似符合以下三种函数模型之一:
近似符合以下三种函数模型之一: ![]() =
=![]() =
=![]() =
= ![]() .
.
(1)找出你认为最适合的函数模型,并说明理由,然后选取其中你认为最适合的数据求出相应的解析式;
(2)因遭受某国对该产品进行反倾销的影响,2015年的年产量比预计减少![]() ,试根据所建立的函数模型,确定2015年的年产量.
,试根据所建立的函数模型,确定2015年的年产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aln(x+1)+ ![]() x2﹣x,其中a为实数.
x2﹣x,其中a为实数.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)若函数f(x)有两个极值点x1 , x2 , 且x1<x2 , 求证:2f(x2)﹣x1>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com