
若函数 在区间
在区间 上单调递减,则实数
上单调递减,则实数 的取值范围为______.
的取值范围为______.
【解析】
试题分析:将函数化成分段函数的形式,不难得到它的减区间为(2,3).结合题意得:(5a,4a+1)?(2,3),由此建立不等关系,解之即可得到实数a的取值范围.解:函数f(x)=|x-2|(x-4)
="(x-2)(x-4)" (x≥2)
(2-x)(x-4) (x<2)
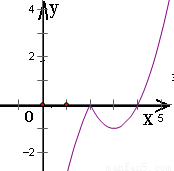
∴函数的增区间为(-∞,2)和(3,+∞),减区间是(2,3).∵在区间(5a,4a+1)上单调递减,∴(5a,4a+1)?(2,3),得2≤5a, 4a+1≤3,解之得 ≤a≤
≤a≤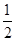
故答案为: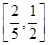
考点:含有绝对值的函数
点评:本题给出含有绝对值的函数,在已知减区间的情况下求参数a的取值范围,着重考查了函数的单调性和单调区间求法等知识,属于中档题


科目:高中数学 来源:2011-2012学年安徽省皖南八校高三第一次联考文科数学试卷解析版 题型:解答题
(本小题满分13分)已知函数
(I)求函数 的单调区间;
的单调区间;
(II)若
 ,在(1,2)上为单调递
,在(1,2)上为单调递
减函数。求实数a的范围。
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试理科数学(北京卷解析版) 题型:解答题
已知函数 ,(
,( ),
),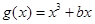
(1)若曲线 与曲线
与曲线 在它们的交点(1,c)处具有公共切线,求a,b的值
在它们的交点(1,c)处具有公共切线,求a,b的值
(2)当 时,若函数
时,若函数 的单调区间,并求其在区间(-∞,-1)上的最大值。
的单调区间,并求其在区间(-∞,-1)上的最大值。
【解析】(1) ,
,
∵曲线 与曲线
与曲线 在它们的交点(1,c)处具有公共切线
在它们的交点(1,c)处具有公共切线
∴ ,
,
∴
(2)令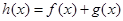 ,当
,当 时,
时,
 令
令 ,得
,得
 时,
时,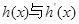 的情况如下:
的情况如下:
|
x |
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
|
|
|
|
所以函数 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为
当 ,即
,即 时,函数
时,函数 在区间
在区间 上单调递增,
上单调递增, 在区间
在区间 上的最大值为
上的最大值为 ,
,
当 且
且 ,即
,即 时,函数
时,函数 在区间
在区间 内单调递增,在区间
内单调递增,在区间 上单调递减,
上单调递减, 在区间
在区间 上的最大值为
上的最大值为
当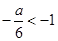 ,即a>6时,函数
,即a>6时,函数 在区间
在区间 内单调递赠,在区间
内单调递赠,在区间 内单调递减,在区间
内单调递减,在区间 上单调递增。又因为
上单调递增。又因为
所以 在区间
在区间 上的最大值为
上的最大值为 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com