
【题目】已知向量![]() ,记
,记![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)在锐角![]() 中,角
中,角![]() 的对边分别是
的对边分别是![]() ,且满足
,且满足![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 为正方形,
为正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
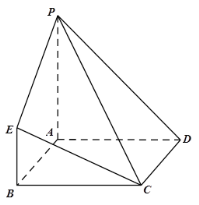
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?如果存在,求
?如果存在,求![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一农产品近六年的产量统计如下表:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 5.1 | 5.3 | 5.6 | 5.5 | 6.0 | 6.1 |
观察表中数据看出,可用线性回归模型拟合![]() 与
与![]() 的关系.
的关系.
(1)根据表中数据,将以下表格空白部分的数据填写完整,并建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
|
|
|
|
|
| 总和 | 均值 | |
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 5.1 | 5.3 | 5.6 | 5.5 | 6.0 | 6.1 | ||
| 1 | 4 | 9 | 16 | 25 | 36 | ||
| 5.1 | 10.6 | 16.8 | 22 | 30 | 36.6 | 121.1 |
(2)若在2025年之前该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() 满足的关系式为
满足的关系式为![]() ,且每年该农产品都能全部销售.预测在2013~2025年之间,某市该农产品的销售额
,且每年该农产品都能全部销售.预测在2013~2025年之间,某市该农产品的销售额![]() 在哪一年达到最大.
在哪一年达到最大.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: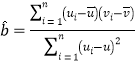
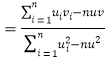 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是一个直角梯形,其中
是一个直角梯形,其中![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,点M和点N分别为
,点M和点N分别为![]() 和
和![]() 的中点.
的中点.
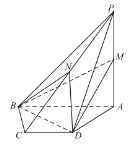
(1)证明:直线![]() 平面
平面![]() ;
;
(2)求直线![]() 和平面
和平面![]() 所成角的余弦值;
所成角的余弦值;
(3)求二面角![]() 的正弦值;
的正弦值;
(4)求点P到平面![]() 的距离;
的距离;
(5)设点N在平面![]() 内的射影为点H,求线段
内的射影为点H,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为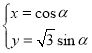 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若点![]() 在曲线
在曲线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 的最小值及此时点
的最小值及此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com