
【题目】解关于![]() 的不等式
的不等式![]() .
.
【答案】当![]() 时,解集为:R ;当
时,解集为:R ;当![]() 时,解集为:
时,解集为:![]() ;当
;当![]() 时,解集为
时,解集为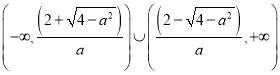 ;当
;当![]() 时,解集为
时,解集为![]() ; 当
; 当![]() 时,解集为
时,解集为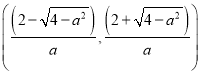 ;当
;当![]() 时,不等式的解集为:
时,不等式的解集为:![]() .
.
【解析】
对参数![]() 展开讨论,从而求解不等式.
展开讨论,从而求解不等式.
(1)当![]() 时,原不等式等价于
时,原不等式等价于![]() ,
,
解得![]() ,故不等式解集为
,故不等式解集为![]() ;
;
(2)当![]() 时,原不等式为二次不等式,
时,原不等式为二次不等式,![]() ,
,
①当![]() 时,即
时,即![]() 时,
时,
不等式对应的方程![]() 有两个不相等实根,
有两个不相等实根,
解得: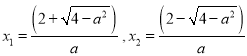
当![]() 时,
时,![]() ,故
,故
不等式的解集为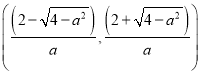 ;
;
当![]() 时,
时,![]() ,故
,故
不等式的解集为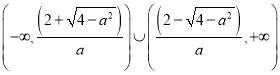
②当![]() 时,即
时,即![]() 时,
时,
不等式对应的方程![]() 有两个相等的实根,
有两个相等的实根,
即![]()
当![]() 时,不等式的解集为:
时,不等式的解集为:![]()
当![]() 时,不等式的解集为:
时,不等式的解集为:![]() .
.
③当![]() 时,即
时,即![]() 时,
时,
不等式对应的方程![]() 没有实数根,故
没有实数根,故
当![]() 时,不等式的解集为:R.
时,不等式的解集为:R.
当![]() 时,不等式的解集为:
时,不等式的解集为:![]() .
.
综上所述: 当![]() 时,解集为:R
时,解集为:R
当![]() 时,解集为:
时,解集为:![]() .
.
当![]() 时,解集为
时,解集为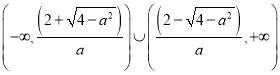
当![]() 时,解集为
时,解集为![]()
当![]() 时,解集为
时,解集为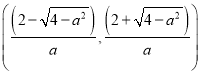
当![]() 时,不等式的解集为:
时,不等式的解集为:![]() .
.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
⑴若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
⑵当![]() ,求函数
,求函数![]() 的最小值
的最小值![]() ;
;
⑶是否存在实数![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,且抛物线的准线被椭圆
的焦点重合,且抛物线的准线被椭圆![]() 截得的弦长为1,
截得的弦长为1,![]() 是直线
是直线![]() 上一点,过点
上一点,过点![]() 且与
且与![]() 垂直的直线交椭圆于
垂直的直线交椭圆于![]() 两点.
两点.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证:![]() 成等差数列.
成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,且点
,且点![]() 和
和![]() 分别为
分别为![]() 和
和![]() 的中点
的中点

(I)求证:![]() 平面
平面![]() ;
;
(II)求二面角![]() 的正弦值;
的正弦值;
(III)设![]() 为棱
为棱![]() 上的点,若直线
上的点,若直线![]() 和平面
和平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的长。
的长。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校命制了一套调查问卷(试卷满分均为100分),并对整个学校的学生进行了测试,先从这些学生的成绩中随机抽取了50名学生的成绩,按照![]() 分成5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分)
分成5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分)
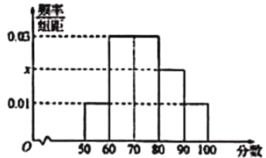
(1)求频率分布直方图中的![]() 的值,并估计50名学生的成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表)
的值,并估计50名学生的成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表)
(2)用样本估计总体,若该校共有2000名学生,试估计该校这次成绩不低于70分的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() :
:![]() 的左焦点,O为坐标原点,
的左焦点,O为坐标原点,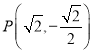 为椭圆上的点.
为椭圆上的点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若点![]() 都在椭圆
都在椭圆![]() 上,且
上,且![]() 中点
中点![]() 在线段
在线段![]() (不包括端点)上,求
(不包括端点)上,求![]() 面积的最大值,及此时直线
面积的最大值,及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取![]() 名学生,将他们的期中考试数学成绩(满分
名学生,将他们的期中考试数学成绩(满分![]() 分,成绩均为不低于
分,成绩均为不低于![]() 分的整数)分成六段:
分的整数)分成六段:![]() ,
,![]() ,…,
,…,![]() 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.
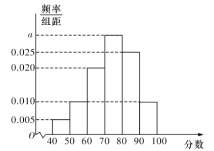
(1)求图中实数![]() 的值;
的值;
(2)若从数学成绩在![]() 与
与![]() 两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于
两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com