
【题目】十九大以来,某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领农村地区人民群众脱贫奔小康,扶贫办计划为某农村地区购买农机机器,假设该种机器使用三年后即被淘汰.农机机器制造商对购买该机器的客户推出了两种销售方案:
方案一:每台机器售价7000元,三年内可免费保养2次,超过2次每次收取保养费200元;
方案二:每台机器售价7050元,三年内可免费保养3次,超过3次每次收取保养费100元.
扶贫办需要决策在购买机器时应该选取那种方案,为此搜集并整理了50台这种机器在三年使用期内保养的次数,得下表:
保养次数 | 0 | 1 | 2 | 3 | 4 | 5 |
台数 | 1 | 10 | 19 | 14 | 4 | 2 |
记![]() 表示1台机器在三年使用期内的保养次数.
表示1台机器在三年使用期内的保养次数.
(1)用样本估计总体的思想,求“![]() 不超过2”的概率;
不超过2”的概率;
(2)若![]() 表示1台机器的售价和三年使用期内花费的费用总和(单位:元),求选用方案一时
表示1台机器的售价和三年使用期内花费的费用总和(单位:元),求选用方案一时![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)按照两种销售方案,分别计算这50台机器三年使用期内的总费用(总费用=售价+保养费),以每台每年的平均费用作为决策依据,扶贫办选择那种销售方案购买机器更合算?
【答案】(1)0.6;(2)![]() ;(3)355600,353300,第二种方案.
;(3)355600,353300,第二种方案.
【解析】
(1)根据表中所给数据可得“![]() 不超过2”的频数,利用古典概型概率公式可求“
不超过2”的频数,利用古典概型概率公式可求“![]() 不超过2”的概率;(2)当
不超过2”的概率;(2)当![]() 时,
时,![]() ;当
;当![]() ,
,![]() ,从而可得结果;(3)求出方案一中,这50台机器售价和保养总费用可得每年每台的平均费用,求出方案二中,这50台机器售价和保养总费用,可得每年每台的平均费用,比较两种方案每年每台的平均费用的大小,从而可得结果,
,从而可得结果;(3)求出方案一中,这50台机器售价和保养总费用可得每年每台的平均费用,求出方案二中,这50台机器售价和保养总费用,可得每年每台的平均费用,比较两种方案每年每台的平均费用的大小,从而可得结果,
(1)从上表中可以看出50台机器维修次数不超过2次的台数共30台,故“![]() 不超过2”的概率为
不超过2”的概率为![]() .
.
(2)当![]() 时,
时,![]() ;当
;当![]() ,
,![]() ,
,
故![]() 关于
关于![]() 的函数解析式为
的函数解析式为![]() .
.
(3)在方案一中,这50台机器售价和保养总费用为
![]() (元).
(元).
所以每年每台平均费用为![]() 元.
元.
在方案二中,这50台机器售价和保养总费用为![]() (元).
(元).
所以每年每台平均费用为![]() 元.因为
元.因为![]() ,
,
所以扶贫办应选择第二种方案更合算.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】某高校共有10000人,其中男生7500人,女生2500人,为调查该校学生每则平均体育运动时间的情况,采用分层抽样的方法,收集200位学生每周平均体育运动时间的样本数据(单位:小时).调查部分结果如下![]() 列联表:
列联表:
男生 | 女生 | 总计 | |
每周平均体育运动时间不超过4小时 | 35 | ||
每周平均体育运动时间超过4小时 | 30 | ||
总计 | 200 |
(1)完成上述每周平均体育运动时间与性别的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 把握认为“该校学生的每周平均体育运动时间与性别有关”;
把握认为“该校学生的每周平均体育运动时间与性别有关”;
(2)已知在被调查的男生中,有5名数学系的学生,其中有2名学生每周平均体育运动时间超过4小时,现从这5名学生中随机抽取2人,求恰有1人“每周平均体育运动时间超过4小时”的概率.
附: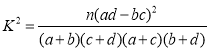 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁分店销售某种商品,每件商品的成本为4元,并且每件商品需向总店交![]() 元的管理费,预计当每件商品的售价为
元的管理费,预计当每件商品的售价为![]() 元时,一年的销售量为
元时,一年的销售量为![]() 万件.
万件.
(1)求该连锁分店一年的利润![]() (万元)与每件商品的售价
(万元)与每件商品的售价![]() 的函数关系式
的函数关系式![]() ;
;
(2)当每件商品的售价为多少元时,该连锁分店一年的利润![]() 最大,并求出
最大,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() 为参数),直线
为参数),直线![]() 经过点
经过点![]() ,且倾斜角为
,且倾斜角为![]() .
.
(1)写出直线![]() 的参数方程和圆
的参数方程和圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,右焦点为
,右焦点为![]() ,设M,N是椭圆C上位于x轴上方的两动点,且直线
,设M,N是椭圆C上位于x轴上方的两动点,且直线![]() 与直线
与直线![]() 平行,
平行,![]() 与
与![]() 交于点D.
交于点D.
(Ⅰ)求![]() 和
和![]() 的坐标;
的坐标;
(Ⅱ)求![]() 的最小值;
的最小值;
(Ⅲ)求证:![]() 是定值.
是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的焦点为F,圆
的焦点为F,圆![]() ,点
,点![]() 为抛物线上一动点.已知当
为抛物线上一动点.已知当![]() 的面积为
的面积为![]() .
.

(I)求抛物线方程;
(II)若![]() ,过P做圆C的两条切线分别交y轴于M,N两点,求
,过P做圆C的两条切线分别交y轴于M,N两点,求![]() 面积的最小值,并求出此时P点坐标.
面积的最小值,并求出此时P点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】足球是世界普及率最高的运动,我国大力发展校园足球.为了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校y(百个) | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱.
(已知:![]() ,则认为y与x线性相关性很强;
,则认为y与x线性相关性很强;![]() ,则认为y与x线性相关性一般;
,则认为y与x线性相关性一般;![]() ,则认为y与x线性相关性较):
,则认为y与x线性相关性较):
(2)求y关于x的线性回归方程,并预测A地区2020年足球特色学校的个数(精确到个).
参考公式和数据: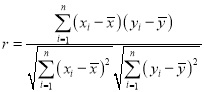 ,
,
![]()
![]()
![]() ,
,
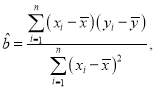
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com