Question

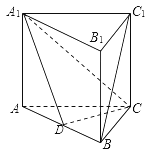
【题目】如图，在正三棱柱ABC-A1B1C1中, D为AB的中点.

（Ⅰ）求证：CD平面ABB1A1；

（Ⅱ）求证：BC1∥平面A1CD.

Answer 1

【答案】(1) 证明见解析.

(2) 证明见解析.

【解析】分析：（Ⅰ）通过线面垂直的性质，可以利用CD垂直AB，CD垂直AA1来证明CD垂直平面ABB1A1。（Ⅱ）通过利用中线定理，可以得到BC1 //OD，又由线面平行的判断可以推出，B C1// 平面 A 1C D.

详解：(Ⅰ)因为正三棱柱 ABC-A1B1C1， D为 AB的中点，

所以 CD⊥AB， AA1⊥底面 ABC.又因为 CD底面 ABC，

所以 AA1⊥CD.

又因为 AA1AB=A,AB平面 ABB1A1， AA1平面 ABB1A1，

所以 CD⊥平面 ABB1A1.

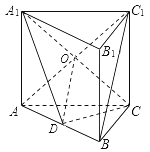
(Ⅱ)连接 AC1，设 A1CAC1=O，连接 OD，

由正三棱柱 ABC-A1B1C1，得 AO=OC1，

又因为在 ABC-A1B1C1中，AD=DB ，

所以 OD//BC1

又因为BC1平面 A1CD， OD平面 A1CD，

所以 BC1//平面 A1CD.