
【题目】(12分)如图,底面是正三角形的直三棱柱![]() 中,D是BC的中点,
中,D是BC的中点,![]() .
.
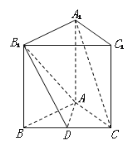
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求的A1 到平面![]() 的距离.
的距离.
【答案】(Ⅰ)参考解析,(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)需证明![]() 平面
平面![]() ,只需要在平面
,只需要在平面![]() 上找到一条直线与
上找到一条直线与![]() 平行,通过三角形的中位线可得以上结论.
平行,通过三角形的中位线可得以上结论.
(Ⅱ)需求点到面的距离,本题通过构建一个三棱锥,让其体积算两次即得到一个等式,即可取出结论.解法一通过三棱锥![]() 与三棱锥
与三棱锥![]() 的体积相等,由体积公式即可求得结论;解法二由(Ⅰ)得到的线面平行转化为三棱锥
的体积相等,由体积公式即可求得结论;解法二由(Ⅰ)得到的线面平行转化为三棱锥![]() 与三棱锥
与三棱锥![]() 体积相等,从而得到结论.
体积相等,从而得到结论.
试题解析:(1)连接![]() 交
交![]() 于O,连接OD,在
于O,连接OD,在![]() 中,O为
中,O为![]() 中点,D为BC中点
中点,D为BC中点
![]() 3分
3分
![]()
![]() 6分
6分
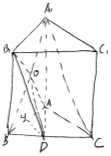
(2)解法一:设![]() 点到平面
点到平面![]() 的距离为h
的距离为h
在![]() 中,
中,![]()
![]()
![]()
![]() 为
为![]()
![]() 8分
8分
![]()
过D作![]() 于H
于H
又![]() 为直棱柱
为直棱柱
![]()
![]() 且
且![]() 10分
10分
![]()
即![]()
解得![]() 12分
12分
解法二:由①可知![]()
![]() 点
点![]() 到平面
到平面![]() 的距离等于点C到平面
的距离等于点C到平面![]() 的距离 8分
的距离 8分
![]() 为
为![]()
![]()
![]() 10分
10分
设点C到面![]() 的距离为h
的距离为h
![]()
即![]()
解得![]() 12分
12分


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】如图,在棱长为ɑ 的正方体ABCD﹣A1B1C1D1中,E、F、G分别是CB.CD.CC1的中点. 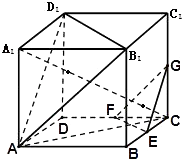
(1)求直线 A1C与平面ABCD所成角的正弦的值;
(2)求证:平面A B1D1∥平面EFG.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子装有六张卡片,上面分别写着如下六个函数: ![]() .
.
(I)判断这![]() 个函数的奇偶性;
个函数的奇偶性;
(II)从中任意拿取两张卡片,若其中至少有一张卡片上写着的函数为奇函数.在此条件下,求两张卡片上写着的函数相加得到的新函数为奇函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,已知PA⊥平面ABCD,AD∥BC,AD⊥AB,PA=AD=2BC=2AB=2. 
(1)求证:平面PAC⊥平面PCD;
(2)若E是PD的中点,求平面BCE将四棱锥P﹣ABCD分成的上下两部分体积V1、V2之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆x2+4y2=4,直线l:y=x+m
(1)若l与椭圆有一个公共点,求m的值;
(2)若l与椭圆相交于P、Q两点,且|PQ|等于椭圆的短轴长,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公务员招聘中,既有笔试又有面试,某单位在2015年公务员考试中随机抽取100名考生的笔试成绩,按成绩分为5组[50,60),[60,70),[70,80),[80,90),[90,100],得到的频率分布直方图如图所示. 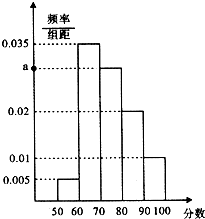
(1)求a值及这100名考生的平均成绩;
(2)若该单位决定在成绩较高的第三、四、五组中按分层抽样抽取6名考生进入第二轮面试,现从这6名考生中抽取3名考生接受单位领导面试,设第四组中恰有1名考生接受领导面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A、B、C所对边的长分别为a、b、c,则下列命题:
①若ab>c2 , 则C ![]() ;
;
②若a+b>2c,则C ![]() ;
;
③若a3+b3=c3 , 则C ![]() ;
;
④若(a+b)c<2ab,则ab>c2;
⑤若(a2+b2)c2<2a2b2 , 则C ![]() .
.
其中正确命题是(写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
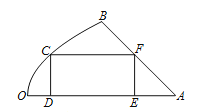
【题目】如图是一块地皮![]() ,其中
,其中![]() ,
, ![]() 是直线段,曲线段
是直线段,曲线段![]() 是抛物线的一部分,且点
是抛物线的一部分,且点![]() 是该抛物线的顶点,
是该抛物线的顶点, ![]() 所在的直线是该抛物线的对称轴.经测量,
所在的直线是该抛物线的对称轴.经测量, ![]() km,
km, ![]() km,
km, ![]() .现要从这块地皮中划一个矩形
.现要从这块地皮中划一个矩形![]() 来建造草坪,其中点
来建造草坪,其中点![]() 在曲线段
在曲线段![]() 上,点
上,点![]() ,
, ![]() 在直线段
在直线段![]() 上,点
上,点![]() 在直线段
在直线段![]() 上,设
上,设![]() km,矩形草坪
km,矩形草坪![]() 的面积为
的面积为![]() km2.
km2.
(1)求![]() ,并写出定义域;
,并写出定义域;
(2)当![]() 为多少时,矩形草坪
为多少时,矩形草坪![]() 的面积最大?
的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数F(x)= ![]() ,其中f(x)=log2(x2+1),g(x)=log2(|x|+7).
,其中f(x)=log2(x2+1),g(x)=log2(|x|+7).
(1)在实数集R上用分段函数形式写出函数F(x)的解析式;
(2)求函数F(x)的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com