
【题目】如图,在四棱锥P﹣ABCD中,已知PA⊥平面ABCD,AD∥BC,AD⊥AB,PA=AD=2BC=2AB=2. 
(1)求证:平面PAC⊥平面PCD;
(2)若E是PD的中点,求平面BCE将四棱锥P﹣ABCD分成的上下两部分体积V1、V2之比.
【答案】
(1)证明:∵PA⊥平面ABCD,CD平面ABCD,
∴PA⊥CD.
取AD中点H,连接CH,则CH⊥AD,CH=AB=HD.
∴∠ACH=∠DCH=45°,
∴AC⊥CD,
∵PA∩AC=A,
∴CD⊥平面PAC,
∵CD平面PAC,
∴平面PAC⊥平面PCD;
(2)证明:解:取PD中点E,PA中点F,连接EF,BE,则EF∥AD,
∵BC∥AD,
∴EF∥BC,
∴B,C,E,F四点共面.
故平面BCE将四棱锥P﹣ABCD分成的上部分为四棱锥P﹣BCEF,下部分为多面体EFABCD.
易知ABF﹣HCE为直三棱柱,CH⊥平面PAD.
∴V2=VABF﹣HCE+VC﹣DEH=S△ABFBC+ ![]() =
= ![]() +
+ ![]()
= ![]() =
= ![]() ,
,
∵VP﹣ABCD= ![]() =
= ![]() =1,
=1,
∴V1=1﹣ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() .
.

【解析】(1)取AD中点H,连接CH,则CH⊥AD,CH=AB=HD,证明CD⊥平面PAC,即可证明求证:平面PAC⊥平面PCD;(2)证明B,C,E,F四点共面,故平面BCE将四棱锥P﹣ABCD分成的上部分为四棱锥P﹣BCEF,下部分为多面体EFABCD.易知ABF﹣HCE为直三棱柱,CH⊥平面PAD,利用体积公式,即可求平面BCE将四棱锥P﹣ABCD分成的上下两部分体积V1、V2之比.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(2)设函数![]() ,
, ![]() .若函数
.若函数![]() 的最小值是
的最小值是![]() ,求
,求![]() 的值;
的值;
(3)若函数![]() ,
, ![]() 的定义域都是
的定义域都是![]() ,对于函数
,对于函数![]() 的图象上的任意一点
的图象上的任意一点![]() ,在函数
,在函数![]() 的图象上都存在一点
的图象上都存在一点![]() ,使得
,使得![]() ,其中
,其中![]() 是自然对数的底数,
是自然对数的底数, ![]() 为坐标原点.求
为坐标原点.求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() ,抛物线
,抛物线![]() ,
, ![]() 与
与![]() 有公共的焦点
有公共的焦点![]() ,
, ![]() 与
与![]() 在第一象限的公共点为
在第一象限的公共点为![]() ,直线
,直线![]() 的倾斜角为
的倾斜角为![]() ,且
,且![]() ,则关于双曲线的离心率的说法正确的是()
,则关于双曲线的离心率的说法正确的是()
A. 仅有两个不同的离心率![]() 且
且![]() B. 仅有两个不同的离心率
B. 仅有两个不同的离心率![]() 且
且![]() C. 仅有一个离心率
C. 仅有一个离心率![]() 且
且![]() D. 仅有一个离心率
D. 仅有一个离心率![]() 且
且![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把边长为2的正方形ABCD沿对角线BD折起并连接AC形成三棱锥C﹣ABD,其正视图、俯视图均为等腰直角三角形(如图所示),则三棱锥C﹣ABD的表面积为 . 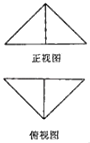
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈A,且A={x|a﹣1<x<a+1},命题q:x∈B,且B={x|x2﹣4x+3≥0}
(Ⅰ)若A∩B=,A∪B=R,求实数a的值;
(Ⅱ)若p是q的充分条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com