
【题目】已知函数![]() .
.
(I)当a=-1时,
①求曲线y= f(x)在点(0,f(0))处的切线方程;
②求函数f(x)的最小值;
(II)求证:当![]() 时,曲线
时,曲线![]() 与
与![]() 有且只有一个交点.
有且只有一个交点.
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,其焦距为
,其焦距为![]() ,点E为椭圆的上顶点,且
,点E为椭圆的上顶点,且![]() .
.
(1)求椭圆C的方程;
(2)设圆![]() 的切线l交椭圆C于A,B两点(O为坐标原点),求证
的切线l交椭圆C于A,B两点(O为坐标原点),求证![]() ;
;
(3)在(2)的条件下,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节期间爆发的新型冠状病毒(COVID-19)是新中国成立以来感染人数最多的一次疫情.一个不知道自己已感染但处于潜伏期的甲从疫区回到某市过春节,回到家乡后与朋友乙、丙、丁相聚过,最终乙、丙、丁也感染了新冠病毒.可以肯定的是乙受甲感染的,丙是受甲或乙感染的,假设他受甲和受乙感染的概率分别是![]() 和
和![]() .丁是受甲、乙或丙感染的,假设他受甲、乙和丙感染的概率分别是
.丁是受甲、乙或丙感染的,假设他受甲、乙和丙感染的概率分别是![]() 、
、![]() 和
和![]() .在这种假设之下,乙、丙、丁中直接受甲感染的人数为
.在这种假设之下,乙、丙、丁中直接受甲感染的人数为![]() .
.
(1)求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)该市在发现在本地出现新冠病毒感染者后,迅速采取应急措施,其中一项措施是各区必须每天及时,上报新增疑似病例人数.![]() 区上报的连续
区上报的连续![]() 天新增疑似病例数据是“总体均值为
天新增疑似病例数据是“总体均值为![]() ,中位数
,中位数![]() ”,
”,![]() 区上报的连续
区上报的连续![]() 天新增疑似病例数据是“总体均值为
天新增疑似病例数据是“总体均值为![]() ,总体方差为
,总体方差为![]() ”.设
”.设![]() 区和
区和![]() 区连续
区连续![]() 天上报新增疑似病例人数分别为
天上报新增疑似病例人数分别为![]() 和
和![]() ,
,![]() 和
和![]() 分别表示
分别表示![]() 区和
区和![]() 区第
区第![]() 天上报新增疑似病例人数(
天上报新增疑似病例人数(![]() 和
和![]() 均为非负).记
均为非负).记![]() ,
,![]() .
.
①试比较![]() 和
和![]() 的大小;
的大小;
②求![]() 和
和![]() 中较小的那个字母所对应的
中较小的那个字母所对应的![]() 个数有多少组?
个数有多少组?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,M,M1分别为AB,A1B1中点.
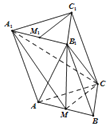
(1)求证:C1M1∥面A1MC;
(2)若面ABC⊥面ABB1A1,△AB1B为正三角形,AB=2,BC=1,![]() ,求四棱锥B1﹣AA1C1C的体积.
,求四棱锥B1﹣AA1C1C的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() ,
,![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 在
在![]() 处的切线平行于
处的切线平行于![]() 轴,是否存在整数
轴,是否存在整数![]() ,使不等式
,使不等式![]() 在
在![]() 时恒成立?若存在,求出
时恒成立?若存在,求出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大自然是非常奇妙的,比如蜜蜂建造的蜂房.蜂房的结构如图所示,开口为正六边形ABCDEF,侧棱AA'、BB'、CC'、DD'、EE'、FF'相互平行且与平面ABCDEF垂直,蜂房底部由三个全等的菱形构成.瑞士数学家克尼格利用微积分的方法证明了蜂房的这种结构是在相同容积下所用材料最省的,因此,有人说蜜蜂比人类更明白如何用数学方法设计自己的家园.英国数学家麦克劳林通过计算得到∠B′C′D′=109°28′16'.已知一个房中BB'=5![]() ,AB=2
,AB=2![]() ,tan54°44′08'
,tan54°44′08'![]() ,则此蜂房的表面积是_____.
,则此蜂房的表面积是_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)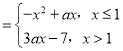 ,若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,则实数a的取值范围是( )
,若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,则实数a的取值范围是( )
A.[3,+∞)B.(3,+∞)C.(﹣∞,3)D.(﹣∞,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在抗击新冠肺炎疫情期间,很多人积极参与了疫情防控的志愿者活动.各社区志愿者服务类型有:现场值班值守,社区消毒,远程教育宣传,心理咨询(每个志愿者仅参与一类服务).参与A,B,C三个社区的志愿者服务情况如下表:
社区 | 社区服务总人数 | 服务类型 | |||
现场值班值守 | 社区消毒 | 远程教育宣传 | 心理咨询 | ||
A | 100 | 30 | 30 | 20 | 20 |
B | 120 | 40 | 35 | 20 | 25 |
C | 150 | 50 | 40 | 30 | 30 |
(1)从上表三个社区的志愿者中任取1人,求此人来自于A社区,并且参与社区消毒工作的概率;
(2)从上表三个社区的志愿者中各任取1人调查情况,以X表示负责现场值班值守的人数,求X的分布列;
(3)已知A社区心理咨询满意率为0.85,B社区心理咨询满意率为0.95,C社区心理咨询满意率为0.9,“![]() ,
,![]() ,
,![]() ”分别表示A,B,C社区的人们对心理咨询满意,“
”分别表示A,B,C社区的人们对心理咨询满意,“![]() ,
,![]() ,
,![]() ”分别表示A,B,C社区的人们对心理咨询不满意,写出方差
”分别表示A,B,C社区的人们对心理咨询不满意,写出方差![]() ,
,![]() ,
,![]() 的大小关系.(只需写出结论)
的大小关系.(只需写出结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com