
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)讨论![]() 单调性;
单调性;
(Ⅱ)当![]() 时,设函数
时,设函数![]() 存在两个零点
存在两个零点![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)详见解析;(Ⅱ)证明见解析
【解析】
(Ⅰ)![]() ,分
,分![]() 和
和![]() 两种情况讨论函数的单调性;
两种情况讨论函数的单调性;
(Ⅱ)解法一:由题意可知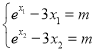 ,两式相减可得
,两式相减可得![]() ,再利用分析法转化为证明要证
,再利用分析法转化为证明要证![]() ,只需证
,只需证![]() ,再通过变形,构造,证明只需证
,再通过变形,构造,证明只需证![]() 即可,
即可,![]() ,构造函数
,构造函数![]() ,利用导数证明
,利用导数证明![]() .
.
解法二:由题意可知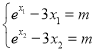 ,再换元令
,再换元令![]() ,即
,即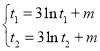 ,两式相减得
,两式相减得![]() ,要证
,要证![]() ,即只需证
,即只需证![]() ,即证
,即证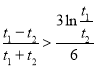 ,再通过变形,构造得到
,再通过变形,构造得到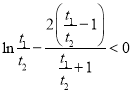 ,
,![]() ,
,![]() ,利用导数证明
,利用导数证明![]() .
.
解:(1)![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,令
时,令![]() 得
得![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
(Ⅱ)解法一:由题意知![]() ,由
,由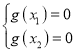 得
得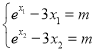 ,
,
两式相减得![]() ,因为
,因为![]() ,故
,故![]() ,
,
要证![]() ,只需证
,只需证![]() ,
,
两边同除以![]() 得
得![]() ,
,
令![]() ,故只需证
,故只需证![]() 即可.
即可.
令![]() ,
,![]() ,
,
令![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递减,
上单调递减,
故![]() ,故
,故![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,故原命题得证.
,故原命题得证.
【解法二】
由题意知![]() ,由
,由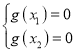 得
得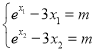 ,
,
令![]() ,即
,即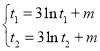 ,两式相减得
,两式相减得![]() ,
,
要证![]() ,即只需证
,即只需证![]() ,即证
,即证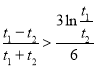 ,即
,即![]() ,即
,即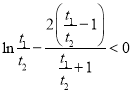 ,
,
令![]() ,只需证
,只需证![]() 即可.
即可.
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,因此原不等式成立.
,因此原不等式成立.


科目:高中数学 来源: 题型:
【题目】设椭圆![]() 长轴长为4,右焦点
长轴长为4,右焦点![]() 到左顶点的距离为3.
到左顶点的距离为3.
(1)求椭圆![]() 的方程;
的方程;
(2)设过原点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点(
两点(![]() 不在坐标轴上),连接
不在坐标轴上),连接![]() 并延长交椭圆于点
并延长交椭圆于点![]() ,若
,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
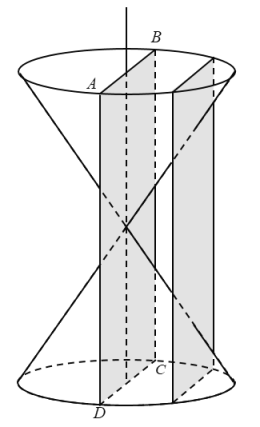
【题目】古希腊数学家阿波罗尼奥斯在他的著作《圆锥曲线论》中记载了用平面切制圆锥得到圆锥曲线的方法.如图,将两个完全相同的圆锥对顶放置(两圆锥的轴重合),已知两个圆锥的底面半径为1,母线长均为![]() ,记过圆锥轴的平面ABCD为平面
,记过圆锥轴的平面ABCD为平面![]() (
(![]() 与两个圆锥面的交线为AC、BD),用平行于
与两个圆锥面的交线为AC、BD),用平行于![]() 的平面截圆锥,该平面与两个圆锥侧面的截线即为双曲线E的一部分,且双曲线E的两条渐近线分别平行于AC、BD,则双曲线E的离心率为( )
的平面截圆锥,该平面与两个圆锥侧面的截线即为双曲线E的一部分,且双曲线E的两条渐近线分别平行于AC、BD,则双曲线E的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
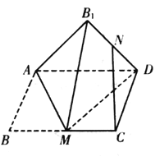
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,连结
,连结![]() ,
,![]() 为
为![]() 的中点,则在翻折过程中,下列说法中所有正确的序号是_______.
的中点,则在翻折过程中,下列说法中所有正确的序号是_______.
①存在某个位置,使得![]() ;
;
②翻折过程中,![]() 的长是定值;
的长是定值;
③若![]() ,则
,则![]() ;
;
④若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 的外接球的表面积是
的外接球的表面积是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全面建成小康社会的决胜阶段,让贫困地区同全国人民共同进入全面小康社会是我们党的庄严承诺.在“脱真贫、真脱贫”的过程中,精准扶贫助推社会公平显得尤其重要.若某农村地区有200户贫困户,经过一年扶贫后,对该地区的“精准扶贫”的成效检查验收.从这200户贫困户中随机抽出50户,对各户的人均年收入(单位:千元)进行调查得到如下频数表:
人均年收入 |
|
|
|
|
|
|
频数 | 2 | 3 | 10 | 20 | 10 | 5 |
若人均年收入在4000元以下的判定为贫困户,人均年收入在4000元~8000元的判定为脱贫户,人均年收入达到8000元的判定为小康户.
(1)用样本估计总体,估计该地区还有多少户没有脱贫;
(2)为了了解未脱贫的原因,从抽取的50户中用分层抽样的方法抽10户进行调研.
①贫困户、脱贫户、小康户分别抽到的人数是多少?
②从被抽到的脱贫户和小康户中各选1人做经验介绍,求小康户中人均年收入最高的一户被选到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,某地援鄂医护人员
日,某地援鄂医护人员![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 人(其中
人(其中![]() 是队长)圆满完成抗击新冠肺炎疫情任务返回本地,他们受到当地群众与领导的热烈欢迎.当地媒体为了宣传他们的优秀事迹,让这
是队长)圆满完成抗击新冠肺炎疫情任务返回本地,他们受到当地群众与领导的热烈欢迎.当地媒体为了宣传他们的优秀事迹,让这![]() 名医护人员和接见他们的一位领导共
名医护人员和接见他们的一位领导共![]() 人站一排进行拍照,则领导和队长站在两端且
人站一排进行拍照,则领导和队长站在两端且![]() 相邻,而
相邻,而![]() 不相邻的排法种数为( )
不相邻的排法种数为( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() ,
,![]() 分别是曲线
分别是曲线![]() ,
,![]() 上两动点且
上两动点且![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com