【题目】一个盒子中装有大小相同的2个白球、3个红球；现从中先后有放回地任取球两次，每次取一个球，看完后放回盒中.
（1）求两次取得的球颜色相同的概率；
（2）若在2个白球上都标上数字1，3个红球上都标上数字2，记两次取得的球上数字之和为
，求的概率分布列与数学期望
.
科目：高中数学 来源： 题型：
【题目】某互联网公司为了确定下一季度的前期广告投入计划，收集了近
个月广告投入量
（单位：万元）和收益
（单位：万元）的数据如下表：
月份 |
|
|
|
|
|
|
广告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他们分别用两种模型①
，②
分别进行拟合，得到相应的回归方程并进行残差分析，得到如图所示的残差图及一些统计量的值：
|
|
|
|
|
|
|
|
（Ⅰ）根据残差图，比较模型①，②的拟合效果，应选择哪个模型？并说明理由；
（Ⅱ）残差绝对值大于
的数据被认为是异常数据，需要剔除：
（ⅰ）剔除异常数据后求出（Ⅰ）中所选模型的回归方程
（ⅱ）若广告投入量
时，该模型收益的预报值是多少？
附：对于一组数据
，
，……，
，其回归直线
的斜率和截距的最小二乘估计分别为：
，
.
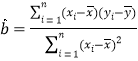
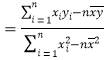查看答案和解析>>
科目：高中数学 来源： 题型：
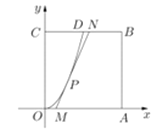
【题目】某城市要建造一个边长为
的正方形市民休闲公园
，将其中的区域
开挖成一个池塘，如图建立平面直角坐标系后，点
的坐标为
，曲线
是函数
图像的一部分，过对边
上一点
的区域
内作一次函数
的图像，与线段
交于点
（点不与点重合），且线段
与曲线有且只有一个公共点
，四边形
为绿化风景区.
（1）写出函数关系式
；
（2）设点的横坐标为
，将四边形的面积
表示成关于的函数
，并求的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给定两个命题，p：对任意实数x都有x2+ax+1≥0恒成立；q：幂函数y=xa-1在（0，+∞）内单调递减；如果p与q中有且仅有一个为真命题，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知双曲线
的左右顶点分别为
.直线
和两条渐近线交于点
,点
在第一象限且
,
是双曲线上的任意一点.
(1)求双曲线的标准方程；
(2)是否存在点P使得
为直角三角形？若存在,求出点P的个数；
(3)直线
与直线
分别交于点
,证明：以
为直径的圆必过定点.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出下列六个命题：
（1）若
，则函数
的图像关于
对称．
（2）函数
与
在区间
上都是增函数．
（3）
的反函数是
（4）
无最大值也无最小值.
（5）
的周期为
.
（6）
有对称轴两条，对称中心三个.
则正确题个数是（ ）
A.1B.2C.3D.4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知等差数列
（公差不为零）和等差数列
，如果关于
的实系数方程
有实数解，那么以下九个方程
（
）中，无实数解的方程最多有（ ）
A.3个B.4个C.5个D.6个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
满足
，对任意的
，都有
.
(1)求数列
的递推公式
(2)数列
满足
，求数列的通项公式;
(3)在(2)的条件下，设
，问是否存在实数
使得数列
是单调递增数列?若存在，求出的取值范围；若不存在，请说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
