练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】给定两个命题，p：对任意实数x都有x2+ax+1≥0恒成立；q：幂函数y=xa-1在（0，+∞）内单调递减；如果p与q中有且仅有一个为真命题，求实数a的取值范围．

    【答案】（-∞，-2）∪[1，2]

    【解析】

    通过两个命题是真命题求出a的范围，然后通过当p真q假时，当p假q真时，即可求解．

    由题意，对任意实数都有x2+ax+1≥0恒成立，则△=a2-4≤0，解得-2≤a≤2，

    幂函数y=xa-1在（0，+∞）内单调递减，可得a-1＜0，解得a＜1，

    由题意知p与q一真一假，

    当p真q假时，有-2≤a≤2且a≥1，得1≤a≤2，

    当p假q真时，有a＜-2或a＞2且a＜1，得a＜-2，

    综上，所求实数a的取值范围是（-∞，-2）∪[1，2]．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知曲线与曲线恰好有两个不同的公共点，则实数的取值范围是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，函数.

    （1）若，求函数在区间上的最大值；

    （2）若，写出函数的单调区间（写出必要的过程，不必证明）；

    （3）若存在，使得关于的方程有三个不相等的实数解，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    (Ⅰ)求函数的单调区间；

    (Ⅱ)设，，若对任意，且，都有，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    (1)讨论的单调性；

    (2)若对于任意的，都有成立，求正整数k的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

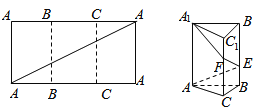
    【题目】如图,把长为6,宽为3的矩形折成正三棱柱,三棱柱的高度为3,矩形的对角线和三棱柱的侧棱的交点记为E,F.

    (1)求三棱柱的体积；

    (2)求三棱柱中异面直线与所成角的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个盒子中装有大小相同的2个白球、3个红球；现从中先后有放回地任取球两次，每次取一个球，看完后放回盒中.

    （1）求两次取得的球颜色相同的概率；

    （2）若在2个白球上都标上数字1，3个红球上都标上数字2，记两次取得的球上数字之和为，求的概率分布列与数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列和满足若为等比数列，且

    （1）求和；

    （2）设，记数列的前项和为

    ①求；

    ②求正整数 k，使得对任意均有.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列、满足，且

    （1）令证明：是等差数列，是等比数列；

    （2）求数列和的通项公式；

    （3）求数列和的前n项和公式．

    查看答案和解析>>

    同步练习册答案