Question

【题目】如图，在三棱锥P﹣ABC中，PC⊥平面ABC，∠ACB=45°，BC=2 ，AB=2．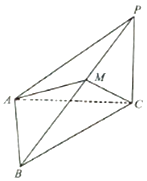
（1）求AC的长；
（2）若PC= ，点M在侧棱PB上，且 = ，当λ为何值时，二面角B﹣AC﹣M的大小为30°．

Answer 1

【答案】
（1）解：在△ABC中，

由余弦定理得AB2=BC2+AC2﹣2BC×AC×cos∠ACB，

得4=8+AC2+﹣4AC，解得AC=2

（2）解：∵PC⊥平面ABC，PA⊥AB，∴AB⊥AC，

以A为原点，AB为x轴，AC为y轴，过A作平面ABC的垂线为z轴，建立空间直角坐标系，

B（2，0，0），C（0，2，0），P（0，2， ），

∵点M在侧棱PB上，且 = ，

∴M（ ， ， ），

设平面ACM的一个法向量为 =（x，y，z），

则 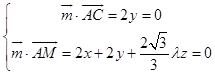，取z=1，得 =（﹣ ，0，1），

平面ABC的一个法向量 =（0，0，1），

∵二面角B﹣AC﹣M的大小为30°，

∴cos30°= = = ，

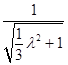解得λ=1或λ=﹣1（舍），

∴当λ=1时，二面角B﹣AC﹣M的大小为30°．

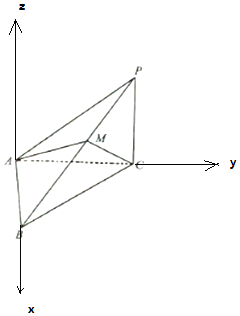
【解析】（1）由已知条件利用余弦定理，利能求出AC．（2）以A为原点，AB为x轴，AC为y轴，过A作平面ABC的垂线为z轴，建立空间直角坐标系，求出平面ACM的一个法向量和平面ABC的一个法向量，利用向量法能求出当λ=1时，二面角B﹣AC﹣M的大小为30°．