
三棱柱 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,
, 分别是
分别是 ,
, 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求三棱锥
 的体积.
的体积.

(1)、(2)见解析;(3)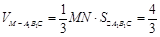 .
.
【解析】判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a⊂α,b⊄α,a∥b⇒a∥α);③利用面面平行的性质定理(α∥β,a⊂α⇒a∥β);④利用面面平行的性质(α∥β,a⊄α, a∥α⇒?a∥β).
解:⑴连结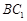 ,
,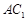 ,
,
∵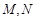 是
是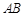 ,
,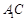 的中点∴
的中点∴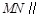
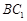 .
.
又∵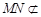 平面
平面 ,∴
,∴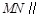 平面
平面 .
. --------------------4分
--------------------4分
⑵∵三棱柱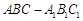 中,侧棱与底面垂直,
中,侧棱与底面垂直,
∴四边形 是正方形.∴
是正方形.∴ .
.
∴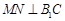 .连结
.连结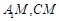 ,
,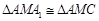 .
.
∴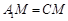 ,又
,又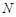 中
中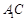 的中点,∴
的中点,∴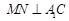 .
.
∵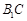 与
与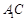 相交于点
相交于点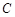 ,∴
,∴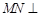 平面
平面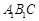 . --------------9分
. --------------9分
⑶由⑵知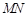 是三棱锥
是三棱锥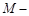
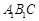 的高.在直角
的高.在直角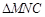 中,
中,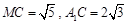 ,
,
∴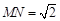 .又
.又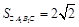 .
.
∴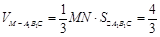 .
--------------------12分
.
--------------------12分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2013-2014学年山西省高三上学期期中考试文科数学试卷(解析版) 题型:解答题
如图,三棱柱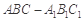 中,侧棱与底面垂直,
中,侧棱与底面垂直,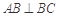 ,
,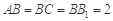 ,
,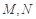 分别是
分别是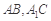 的中点
的中点
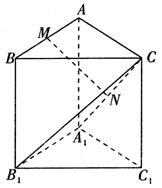
(1)求证: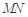 ∥平面
∥平面 ;
;
(2)求证: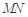 ⊥平面
⊥平面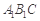 ;
;
(3)求三棱锥的体积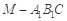 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三下学期模拟冲刺考试文科数学试卷(解析版) 题型:解答题
三棱柱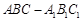 中,侧棱与底面垂直,
中,侧棱与底面垂直,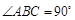 ,
,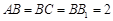 ,
,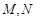 分别是
分别是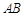 ,
, 的中点.
的中点.
(Ⅰ)求证: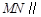 平面
平面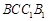 ;
;
(Ⅱ)求证: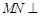 平面
平面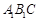 ;
;
(Ⅲ)求三棱锥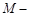
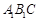 的体积.
的体积.
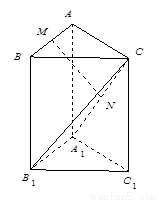
【解析】第一问利连结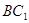 ,
,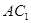 ,∵M,N是AB,
,∵M,N是AB, 的中点∴MN//
的中点∴MN//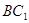 .
.
又∵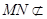 平面
平面 ,∴MN//平面
,∴MN//平面 .
. ----------4分
----------4分
⑵中年∵三棱柱ABC-A1B1C1中,侧棱与底面垂直,∴四边形 是正方形.∴
是正方形.∴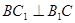 .∴
.∴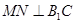 .连结
.连结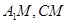 ,
,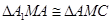 .
.
∴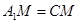 ,又N中
,又N中 的中点,∴
的中点,∴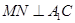 .
.
∵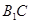 与
与 相交于点C,∴MN
相交于点C,∴MN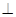 平面
平面 . --------------9分
. --------------9分
⑶中由⑵知MN是三棱锥M- 的高.在直角
的高.在直角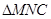 中,
中,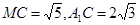 ,
,
∴MN=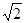 .又
.又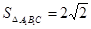 .
.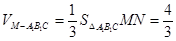 .得到结论。
.得到结论。
⑴连结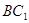 ,
,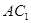 ,∵M,N是AB,
,∵M,N是AB, 的中点∴MN//
的中点∴MN//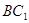 .
.
又∵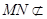 平面
平面 ,∴MN//平面
,∴MN//平面 .
. --------4分
--------4分
⑵∵三棱柱ABC-A1B1C1中,侧棱与底面垂直,
∴四边形 是正方形.∴
是正方形.∴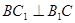 .
.
∴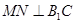 .连结
.连结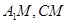 ,
,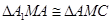 .
.
∴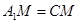 ,又N中
,又N中 的中点,∴
的中点,∴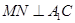 .
.
∵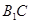 与
与 相交于点C,∴MN
相交于点C,∴MN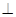 平面
平面 . --------------9分
. --------------9分
⑶由⑵知MN是三棱锥M- 的高.在直角
的高.在直角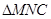 中,
中,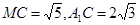 ,
,
∴MN=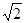 .又
.又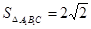 .
.
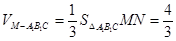
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省湛江市高三下学期第六次月考考试文科数学 题型:解答题
..(本题14分)三棱柱 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,
,  分别是
分别是 ,
, 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求三棱锥
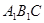 的体积.
的体积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com