
【题目】对于任意给定的无理数![]() 、
、![]() 及实数
及实数![]() ,证明:圆周
,证明:圆周![]() 上至多只有两个有理点(纵、横坐标均为有理数的点)。
上至多只有两个有理点(纵、横坐标均为有理数的点)。
【答案】见解析
【解析】
对于点![]() ,用
,用![]() 表示上述圆周上有理点的个数.
表示上述圆周上有理点的个数.
首先,可以作一个符合条件得圆,其上至少有两个有理点,
为此,取点![]() ,
,![]() .则线段
.则线段![]() 中垂线
中垂线![]() .
.
在直线![]() 上取点
上取点![]() ,再取
,再取![]() .则以
.则以![]() 为圆心、
为圆心、![]() 为半径的圆周上至少有
为半径的圆周上至少有![]() 、
、![]() 这连个有理点.
这连个有理点.
其次说明,对于任何无理点![]() 以及任意正实数
以及任意正实数![]() ,
,![]() .
.
假设有无理点![]() 及正实数
及正实数![]() ,在以
,在以![]() 为圆心、
为圆心、![]() 为半径的圆周上,至少有三个有理点
为半径的圆周上,至少有三个有理点![]() .
.
则![]() . ①
. ①
故![]() , ②
, ②
![]() ③
③
记![]() ,
,![]() .
.
![]() .
.
(1)若![]() ,则由式②知
,则由式②知![]() .
.
由![]() 为无理数,得
为无理数,得![]() .故点
.故点![]() 与
与![]() 重合,矛盾.
重合,矛盾.
类似地,若![]() ,得点
,得点![]() 与
与![]() 重合,矛盾.
重合,矛盾.
(2)若![]() ,
,![]() ,由式②、③消去
,由式②、③消去![]() 得
得
![]() .
.
又![]() 为无理数,故
为无理数,故![]() .
.
则![]() 、
、![]() 、
、![]() 三点共线,这与
三点共线,这与![]() 、
、![]() 、
、![]() 三点共圆矛盾.
三点共圆矛盾.
因此,假设不真,即这种圆上至多有两个有理点.
于是,对于所有的无理点![]() 及所有正实数
及所有正实数![]() ,
,![]() 的最大值为2.
的最大值为2.


科目:高中数学 来源: 题型:
【题目】一只青蛙从数轴的原点出发,当投下的硬币正面向上时,它沿数轴的正方向跳动两个单位;当投下的硬币反面向上时,它沿数轴的负方向跳动一个单位,若青蛙跳动![]() 次停止,设停止时青蛙在数轴上对应的坐标为随机变量
次停止,设停止时青蛙在数轴上对应的坐标为随机变量![]() ,则
,则![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种产品的年固定成本为200万元,每生产![]() 千件,需另投入成本为
千件,需另投入成本为![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,![]() (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,以
中,以![]() 轴为始边做两个锐角
轴为始边做两个锐角![]() ,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为![]()
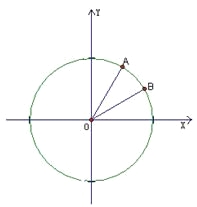
(1)求![]() 的值; (2)求
的值; (2)求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的有( )
A.向量![]() 与
与![]() 是共线向量,则点
是共线向量,则点![]() 、
、![]() 、
、![]() 、
、![]() 必在同一条直线上
必在同一条直线上
B.若![]() 且
且![]() ,则角
,则角![]() 为第二或第四象限角
为第二或第四象限角
C.函数![]() 是周期函数,最小正周期是
是周期函数,最小正周期是![]()
D.![]() 中,若
中,若![]() ,则
,则![]() 为钝角三角形
为钝角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com