
【题目】符号![]() 表示不大于x的最大整数
表示不大于x的最大整数![]() ,例如:
,例如:![]() .
.
(1)解下列两个方程![]() ;
;
(2)设方程: ![]() 的解集为A,集合
的解集为A,集合![]() ,
,![]() ,求实数k的取值范围;
,求实数k的取值范围;
(3)求方程![]() 的实数解.
的实数解.
【答案】(1)![]() ,
,![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() ;
;![]() ;
;![]() ;
;![]() .
.
【解析】
(1)根据对符号![]() 的定义理解可得答案;
的定义理解可得答案;
(2)将![]() 化为
化为![]() ,再分三种情况去绝对值解不等式可得集合
,再分三种情况去绝对值解不等式可得集合![]() ,然后对
,然后对![]() 分类讨论解得集合
分类讨论解得集合![]() ,再根据
,再根据![]() ,列式可求得
,列式可求得![]() 的范围;
的范围;
(3)先判断出![]() ,再将
,再将![]() 平方得
平方得![]() ,再结合方程
,再结合方程![]() 可得不等式
可得不等式![]() ,解不等式可得
,解不等式可得![]() 或
或![]() 或
或![]() 或
或![]() ,分别代入方程
,分别代入方程![]() 可解得答案.
可解得答案.
(1) ![]()
![]() ,
,
(2) ![]() ,
,![]() ,
,
当![]() 时,有
时,有![]() ,解得
,解得 ![]() ,
,
当![]() 时,有
时,有![]() ,
,![]() 无解,
无解,
当![]() 时,有
时,有![]() ,解得:
,解得: ![]()
综上所述:![]() .
.
因为![]()
当![]() 时,
时,![]()
因为![]() ,所以
,所以![]() ,解得
,解得![]() ;
;
当![]() 时,
时,![]() ,
,
因为![]() ,所以
,所以![]() ,解得:
,解得: ![]() ,
,
当![]() 时,
时,![]() ,
,![]() 成立,
成立,
综上: 实数k的取值范围![]() .
.
(3)因![]() , 又
, 又![]() 时,方程
时,方程![]() 不成立,
不成立,
所以![]() ,所以
,所以![]() ,
,
所以![]() ,
,
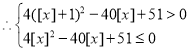 ,
,
所以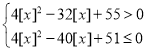
所以![]() ,
,
所以![]() 或
或![]() 且
且![]() ,
,
所以![]() 或
或![]() ,
,
所以![]() 或
或![]() 或
或![]() 或
或![]() ,
,
当![]() 时,原方程化为
时,原方程化为![]() ,所以
,所以![]() ,
,
当![]() 时,原方程化为
时,原方程化为![]() ,所以
,所以![]() ,
,
当![]() 时,原方程化为
时,原方程化为![]() ,
,
当![]() 时,原方程化为
时,原方程化为![]() ,
,
经检验知,这四个值都是原方程的解.
故方程![]() 的实数解为:
的实数解为:![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】设地球表面某地正午太阳高度角为θ,ξ为此时太阳直射纬度,φ为该地的纬度值,则有θ=90°﹣|φ﹣ξ|.根据地理知识,武汉地区的纬度值约为北纬30°,当太阳直射南回归线(此时的太阳直射纬度为﹣23°26')时物体的影子最长,如果在武汉某高度为h0的楼房北边盖一新楼,要使新楼一层正午的太阳全年不被前面的楼房遮挡(如图所示),两楼的距离应至少约为h0的( )倍?(注意tan36°34′=0.75)
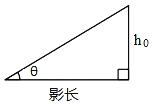
A.0.5倍B.0.8倍C.1倍D.1.4倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱世杰是历史上最伟大的数学家之一,他所著的《四元玉鉴》卷中“如像招数”五问中有如下问题:“今有官司差夫一千八百六十四人筑堤,只云初日差六十四人,次日转多七人,每人日支米三升,共支米四百三石九斗二升,问筑堤几日”。其大意为“官府陆续派遣1864人前往修筑堤坝,第一天派出64人,从第二天开始每天派出的人数比前一天多7人,修筑堤坝的每人每天分发大米3升,共发出大米40392升,问修筑堤坝多少天”,在该问题中前5天共分发了多少大米?
A. 1170升 B. 1380升 C. 3090升 D. 3300升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若![]() 的值域为
的值域为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)巳![]() ,是否存在这祥的实数
,是否存在这祥的实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 内有且只有一个零点.若存在,求出
内有且只有一个零点.若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
(1)终边在y轴上的角的集合是![]() ;
;
(2)把函数f(x)=2sin2x的图象沿x轴方向向左平移![]() 个单位后,得到的函数解析式可以表示成f(x)=2sin
个单位后,得到的函数解析式可以表示成f(x)=2sin![]() ;
;
(3)函数f(x)=![]() sinx+
sinx+![]() 的值域是[-1,1];
的值域是[-1,1];
(4)已知函数f(x)=2cosx,若存在实数x1,x2,使得对任意的实数x都有![]() 成立,则
成立,则![]() 的最小值为2π.
的最小值为2π.
其中正确的命题的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人同时参加一次数学测试,共有20道选择题,每题均有4个选项,答对得3分,答错或不答得0分,甲和乙都解答了所有的试题,经比较,他们只有2道题的选项不同,如果甲最终的得分为54分,那么乙的所有可能的得分值组成的集合为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】疫情期间口罩需求量大增,某医疗器械公司开始生产KN95口罩,并且对所生产口罩的质量按指标测试分数进行划分,其中分数不小于70的为合格品,否则为不合格品,现随机抽取100件口罩进行检测,其结果如下:

(1)根据表中数据,估计该公司生产口罩的不合格率;
(2)根据表中数据,估计该公司口罩的平均测试分数;
(3)若用分层抽样的方式按是否合格从所生产口罩中抽取5件,再从这5件口罩中随机抽取2件,求这2件口罩全是合格品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用合适的方法表示下列集合,并说明是有限集还是无限集.
(1)到A、B两点距离相等的点的集合
(2)满足不等式![]() 的
的![]() 的集合
的集合
(3)全体偶数
(4)被5除余1的数
(5)20以内的质数
(6)![]()
(7)方程![]() 的解集
的解集
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com