
【题目】疫情期间口罩需求量大增,某医疗器械公司开始生产KN95口罩,并且对所生产口罩的质量按指标测试分数进行划分,其中分数不小于70的为合格品,否则为不合格品,现随机抽取100件口罩进行检测,其结果如下:

(1)根据表中数据,估计该公司生产口罩的不合格率;
(2)根据表中数据,估计该公司口罩的平均测试分数;
(3)若用分层抽样的方式按是否合格从所生产口罩中抽取5件,再从这5件口罩中随机抽取2件,求这2件口罩全是合格品的概率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据表中数据确定不合格的口罩数,再利用频数除以总数估计不合格率;
(2)根据平均数计算公式直接求解;
(3)先根据分层抽样确定抽取的5件口罩中不合格的1件,合格的4件,再利用枚举法列出基本事件总数以及至少有一件不合格品包含的基本事件数,最后根据古典概型概率公式以及对立事件概率公式求解.
解:(1)在抽取的100件产品中,不合格的口罩有:4+16=20(件)
所以口罩为不合格品的频率为![]() ,
,
根据频率可估计该公司所生产口罩的不合格率为![]() .
.
(2)平均测试分数为
![]() ·
·
(3)由题意所抽取的5件口罩中不合格的1件,合格的4件.
设4件合格口罩记为a,b,c,d,1件不合格口罩记为x.
若抽取的口罩中恰有1件不合格,则共有ax,bx,cx,dx,4种情况.·
而从5件口罩中抽取2件,共有ab,ac,ad,ax,bc,bd,bx,cd,cx,dx,![]() 种情况.
种情况.
所以2件口罩中至少有一件不合格品的概率为![]() .
.
故2件口罩全是合格品的概率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】2018年“双十一”全网销售额达3143.25亿元,相当于全国人均消费225元,同比增长23.8%,监测参与“双十一”狂欢大促销的22家电商平台有天猫、京东、苏宁易购、网易考拉在内的综合性平台,有拼多多等社交电商平台,有敦煌网、速卖通等出口电商平台.某大学学生社团在本校1000名大一学生中采用男女分层抽样,分别随机调查了若干个男生和60个女生的网购消费情况,制作出男生的频率分布表、直方图(部分)和女生的茎叶图如下:
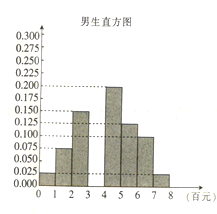
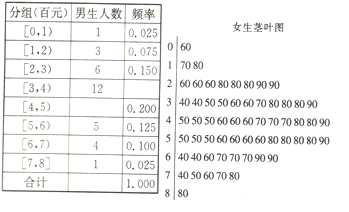
(1)请完成频率分布表的三个空格,并估计该校男生网购金额的中位数(单位:元,精确到个位).
(2)若网购为全国人均消费的三倍以上称为“剁手党”估计该校大一学生中的“剁手党”人数为多少?从抽样数据中网购不足200元的同学中随机抽取2人发放纪念品,则2人都是女生的概率为多少?
(3)用频率估计概率,从全市所有高校大一学生中随机调查5人,求其中“剁手党”人数的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 的普通方程;
的普通方程;
(2)设![]() 是曲线
是曲线![]() 上的一动点,求
上的一动点,求![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双十一”期间,某淘宝店主对其商品的上架时间![]() (小时)和销售量
(小时)和销售量![]() (件)的关系作了统计,得到了如下数据并研究.
(件)的关系作了统计,得到了如下数据并研究.
上架时间 | 2 | 4 | 6 | 8 | 10 | 12 |
销售量 | 64 | 138 | 205 | 285 | 360 | 430 |
(1)求表中销售量![]() 的平均数和中位数;
的平均数和中位数;
(2)① 作出散点图,并判断变量![]() 与
与![]() 是否线性相关?若研究的方案是先根据前5组数据求线性回归方程,再利用第6组数据进行检验,求线性回归方程
是否线性相关?若研究的方案是先根据前5组数据求线性回归方程,再利用第6组数据进行检验,求线性回归方程![]() ;
;
②若根据①中线性回归方程得到商品上架12小时的销售量的预测值与检测值不超过3件,则认为得到的线性回归方程是理想的,试问:①中的线性回归方程是否理想.
附:线性回归方程![]() 中,
中, 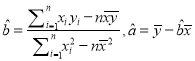 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】底面为菱形的直棱柱![]()
中, ![]()
分别为棱![]()
的中点.
(1)在图中作一个平面![]()
,使得![]()
,且平面![]()
.(不必给出证明过程,只要求作出![]()
与直棱柱![]()
的截面).
(2)若![]()
,求平面![]()
与平面![]()
的距离![]()
.
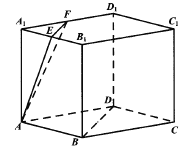
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,其中
,其中![]() 为实常数.
为实常数.
(1)若函数![]() 在区间[2,3]上为单调递增函数,求
在区间[2,3]上为单调递增函数,求![]() 的取值范围;
的取值范围;
(2)高函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,试讨论函数
,试讨论函数![]() ,
,![]() 的零点的情况.
的零点的情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com