
【题目】设函数![]() ,
,![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)讨论函数![]() 的零点个数
的零点个数
【答案】(1)当![]() 时,函数
时,函数![]() 的增区间是
的增区间是![]() 和
和![]() ,减区间是
,减区间是![]() ;
;
当![]() 时,函数
时,函数![]() 的增区间是
的增区间是![]() ,无减区间;
,无减区间;
当![]() 时,函数
时,函数![]() 的增区间是
的增区间是![]() 和
和![]() ,减区间是
,减区间是![]() .
.
(2)当![]() 时,函数
时,函数![]() 存在唯一零点.
存在唯一零点.
【解析】
(1)根据利用导数求函数单调区间的步骤,先求出函数的导数,然后在定义域内解含参的不等式,分类讨论即可求出;
(2)由(1)可知函数的单调性,再结合零点存在性定理即可判断出函数的零点个数.
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]()
当![]() 时,由
时,由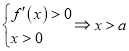 或
或![]() ,由
,由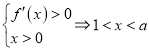 ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,由
时,由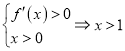 或
或![]() ,
,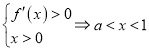
综上,当![]() 时,函数
时,函数![]() 的增区间是
的增区间是![]() 和
和![]() ,减区间是
,减区间是![]() ;
;
当![]() 时,函数
时,函数![]() 的增区间是
的增区间是![]() ,无减区间;
,无减区间;
当![]() 时,函数
时,函数![]() 的增区间是
的增区间是![]() 和
和![]() ,减区间是
,减区间是![]() .
.
(2)由(1)可知,
①当![]() 时,函数
时,函数![]() 在
在![]() 和
和![]() 上递增,在
上递增,在![]() 上递减,
上递减,
所以,![]() ,
,![]() ,但是,
,但是,
当![]() 时,
时,![]() ,存在
,存在![]() ,故
,故![]() ,即在
,即在![]() 上存在唯一零点;
上存在唯一零点;
②当![]() 时,函数
时,函数![]() 在
在![]() 递增,
递增,![]() ,
,![]() ,
,
即在![]() 上存在唯一零点;
上存在唯一零点;
③当![]() 时,函数
时,函数![]() 在
在![]() 和
和![]() 上递增,在
上递增,在![]() 上递减,
上递减,
所以,![]() ,
,![]() ,但是,
,但是,
当![]() 时,
时,![]() ,存在
,存在![]() ,故
,故![]() ,即在
,即在![]() 上存在唯一零点.
上存在唯一零点.
综上,当![]() 时,函数
时,函数![]() 存在唯一零点.
存在唯一零点.


科目:高中数学 来源: 题型:
【题目】一个口袋内有3个不同的红球,4个不同的白球
(1)从中任取3个球,红球的个数不比白球少的取法有多少种?
(2)若取一个红球记2分,取一个白球记1分,从中任取4个球,使总分不少于6分的取法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆盘上有一指针,开始时指向圆盘的正上方.指针每次顺时针方向绕圆盘中心转动一角![]() ,且
,且![]() ,经2004次旋转,第一次回到了其初始位置,即又指向了圆盘的正上方.试问:
,经2004次旋转,第一次回到了其初始位置,即又指向了圆盘的正上方.试问:![]() 有多少个可能的不同值?
有多少个可能的不同值?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l的极坐标方程为θ=α(ρ∈R,ρ≠0),其中α∈[0,π),曲线C1的参数方程为![]() (t为参数),圆C2的普通方程为x2+y2+2
(t为参数),圆C2的普通方程为x2+y2+2![]() x=0.
x=0.
(1)求C1,C2的极坐标方程;
(2)若l与C1交于点A,l与C2交于点B,当|AB|=2时,求△ABC2的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的普及,各类手机娱乐软件也如雨后春笋般涌现. 如表中统计的是某手机娱乐软件自2018年8月初推出后至2019年4月底的月新注册用户数,记月份代码为![]() (如
(如![]() 对应于2018年8月份,
对应于2018年8月份,![]() 对应于2018年9月份,…,
对应于2018年9月份,…,![]() 对应于2019年4月份),月新注册用户数为
对应于2019年4月份),月新注册用户数为![]() (单位:百万人)
(单位:百万人)
![]()
(1)请依据上表的统计数据,判断月新注册用户与月份线性相关性的强弱;
(2)求出月新注册用户关于月份的线性回归方程,并预测2019年5月份的新注册用户总数.
参考数据:![]() ,
,![]() ,
,![]() .
.
回归直线的斜率和截距公式: ,
,![]() .
.
相关系数 (当
(当![]() 时,认为两相关变量相关性很强. )
时,认为两相关变量相关性很强. )
注意:两问的计算结果均保留两位小数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 是两条不同的直线,
是两条不同的直线,![]() 、
、![]() 、
、![]() 是三个不同的平面,则
是三个不同的平面,则![]() 的一个充分条件是( )
的一个充分条件是( )
A.存在一条直线![]() ,
,![]() ,
,![]()
B.存在一条直线![]() ,
,![]() ,
,![]()
C.存在一个平面![]() ,满足
,满足![]() ,
,![]()
D.存在两条异面直线![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com