
【题目】已知函数![]() 在
在![]() 处的切线斜率为
处的切线斜率为![]() .
.
(1)求实数![]() 的值,并讨论函数
的值,并讨论函数![]() 的单调性;
的单调性;
(2)若![]() ,证明:
,证明:![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
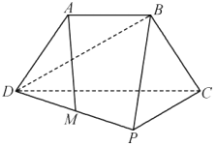
【题目】如图,三角形PCD所在的平面与等腰梯形ABCD所在的平面垂直,AB=AD=![]() CD,AB∥CD,CP⊥CD,M为PD的中点.
CD,AB∥CD,CP⊥CD,M为PD的中点.
(1)求证:AM∥平面PBC;
(2)求证:BD⊥平面PBC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标系与直角坐标系![]() 有相同的长度单位,以原点
有相同的长度单位,以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴.已知曲线
轴正半轴为极轴.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,射线
,射线![]() ,
,![]() ,
,![]() ,
,![]() 与曲线
与曲线![]() 分别交异于极点
分别交异于极点![]() 的四点
的四点![]() ,
,![]() ,
,![]() ,
,![]() .
.
(![]() )若曲线
)若曲线![]() 关于曲线
关于曲线![]() 对称,求
对称,求![]() 的值,并把曲线
的值,并把曲线![]() 和
和![]() 化成直角坐标方程.
化成直角坐标方程.
(![]() )求
)求![]() ,当
,当![]() 时,求
时,求![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年11月2日,中国药品监督管理局批准了治疗阿尔茨海默病(老年痴呆症)新药GV-971的上市申请,这款新药由我国科研人员研发,我国拥有完全知识产权.据悉,该款药品为胶囊,从外观上看是两个半球和一个圆柱组成,其中上半球是胶囊的盖子,粉状药物储存在圆柱及下半球中.胶囊轴截面如图所示,两头是半圆形,中间区域是矩形![]() ,其周长为50毫米,药物所占的体积为圆柱体积和一个半球体积之和.假设
,其周长为50毫米,药物所占的体积为圆柱体积和一个半球体积之和.假设![]() 的长为
的长为![]() 毫米.(注:
毫米.(注:![]() ,
,![]() ,其中
,其中![]() 为球半径,
为球半径,![]() 为圆柱底面积,
为圆柱底面积,![]() 为圆柱的高)
为圆柱的高)
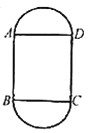
(1)求胶囊中药物的体积![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如何设计![]() 与
与![]() 的长度,使得
的长度,使得![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
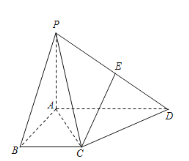
【题目】在四棱锥![]() 中,
中,![]() 平面ABCD,底面ABCD是直角梯形,
平面ABCD,底面ABCD是直角梯形,![]() ,
,![]() ,且
,且![]() ,
,![]() ,点E是线段PD的中点.
,点E是线段PD的中点.
![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() 平面PAB;
平面PAB;
![]() Ⅱ
Ⅱ![]() 求证:平面
求证:平面![]() 平面PCD;
平面PCD;
![]() Ⅲ
Ⅲ![]() 当直线PC与平面PAD所成的角大小为
当直线PC与平面PAD所成的角大小为![]() 时,求线段PA的长.
时,求线段PA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com