
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,短轴的一个端点到焦点的距离为
,短轴的一个端点到焦点的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点在直线
的中点在直线![]() 上,求直线
上,求直线![]() 与
与![]() 轴交点纵坐标的最小值.
轴交点纵坐标的最小值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)根据离心率及短轴的一个端点到焦点的距离为![]() ,可得
,可得![]() 的值,进而得椭圆方程。
的值,进而得椭圆方程。
(2)设出点![]() 、
、![]() 及直线方程,并将直线方程与椭圆方程联立,可得韦达定理表达式,根据判别式可得
及直线方程,并将直线方程与椭圆方程联立,可得韦达定理表达式,根据判别式可得![]() ,根据线段
,根据线段![]() 的中点在直线
的中点在直线![]() 上可得
上可得![]() ,进而用k表示出m,结合基本不等式可求得m的最小值。
,进而用k表示出m,结合基本不等式可求得m的最小值。
(1)由已知得椭圆的离心率为![]() ,短轴的一个端点到焦点的距离为
,短轴的一个端点到焦点的距离为![]() ,
,
解得![]() ,
,![]()
所以椭圆![]() 的方程为
的方程为![]()
(2)设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 与
与![]() 轴交点的纵坐标为
轴交点的纵坐标为![]()
设点![]() ,
,![]() ,
,
将直线![]() 的方程与椭圆方程联立
的方程与椭圆方程联立
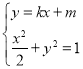 化简得
化简得![]() ,
,
由韦达定理得![]() ,
,![]() ,
,
![]() ,化简得
,化简得![]() .
.
由线段![]() 的中点在直线
的中点在直线![]() 上,得
上,得![]() ,
,
故![]() ,即
,即![]() ,
,
所以![]() ,
,
当且仅当![]() ,即
,即![]() 时取等号,此时
时取等号,此时![]() ,满足
,满足![]() ,
,
因此,直线![]() 与
与![]() 轴交点纵坐标的最小值为
轴交点纵坐标的最小值为![]() .
.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】随着5G商用进程的不断加快,手机厂商之间围绕5G用户的争夺越来越激烈,5G手机也频频降低身价飞人寻常百姓家.某科技公司为了给自己新推出的5G手机定价,随机抽取了100人进行调查,对其在下一次更换5G手机时,能接受的价格(单位:元)进行了统计,得到结果如下表,已知这100个人能接受的价格都在![]() 之间,并且能接受的价格的平均值为2350元(同一组的数据用该组区间的中点值代替).
之间,并且能接受的价格的平均值为2350元(同一组的数据用该组区间的中点值代替).
分组 | 一 | 二 | 三 | 四 | 五 |
手机价格X(元) |
|
|
|
|
|
频数 | 10 | x | y | 20 | 20 |
(1)现用分层抽样的方法从第一、二、三组中随机抽取6人,将该样本看成一个总体,从中随机抽取2人,求其中恰有1人能接受的价格不低于2000元的概率;
(2)若人们对5G手机能接受的价格X近似服从正态分布![]() ,其中
,其中![]() 为样本平均数
为样本平均数![]() ,
,![]() 为样本方差
为样本方差![]() ,求
,求![]() .
.
附:![]() .若
.若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离
的距离![]() ,倾斜角为
,倾斜角为![]() 的直线经过焦点
的直线经过焦点![]() ,且与抛物线交于两点
,且与抛物线交于两点![]() 、
、![]() .
.
(1)求抛物线的标准方程及准线方程;
(2)若![]() 为锐角,作线段
为锐角,作线段![]() 的中垂线
的中垂线![]() 交
交![]() 轴于点
轴于点![]() .证明:
.证明:![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,AD、BE、CF分别为边BC、CA、AB上的高,作以AD为直径的圆T分别与AC、AB交于点M、N,过点M、N作圆T的切线,交于点P,O为△ABC的外心,延长AO,与BC交于点Q,AD与EF交于点R.证明:PD∥QR
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次数学考试后,对高三文理科学生进行抽样调查,调查其对本次考试的结果满意或不满意,现随机抽取![]() 名学生的数据如下表所示:
名学生的数据如下表所示:
满意 | 不满意 | 总计 | |
文科 | 22 | 18 | 40 |
理科 | 48 | 12 | 60 |
总计 | 70 | 30 | 100 |
(1)根据数据,有多大的把握认为对考试的结果满意与科别有关;
(2)用分层抽样方法在感觉不满意的学生中随机抽取![]() 名,理科生应抽取几人;
名,理科生应抽取几人;
(3)在(2)抽取的![]() 名学生中任取2名,求文科生人数的期望.(
名学生中任取2名,求文科生人数的期望.(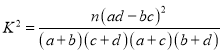 其中
其中![]() )
)
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左
的左![]() 、
、![]() 右焦点分别为,点
右焦点分别为,点![]() 在椭圆上,且满足
在椭圆上,且满足![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设倾斜角为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,求
,求![]() 取最大值时直线
取最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com