
【题目】在直角坐标系xOy中,圆C的参数方程 ![]() (φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线l的极坐标方程是2ρsin(θ+ ![]() )=3
)=3 ![]() ,射线OM:θ=
,射线OM:θ= ![]() 与圆C的交点为O、P,与直线l的交点为Q,求线段PQ的长.
与圆C的交点为O、P,与直线l的交点为Q,求线段PQ的长.
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】已知Sn是等比数列{an}的前n项和,S3 , S9 , S6成等差数列. (Ⅰ)求证:a2 , a8 , a5成等差数列;
(Ⅱ)若等差数列{bn}满足b1=a2=1,b3=a5 , 求数列{an3bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个结论: ①函数 ![]() 的对称中心是(﹣1,2);
的对称中心是(﹣1,2);
②若关于x的方程 ![]() 没有实数根,则k的取值范围是k≥2;
没有实数根,则k的取值范围是k≥2;
③在△ABC中,“bcosA=acosB”是“△ABC为等边三角形”的充分不必要条件;
④若 ![]() 的图象向右平移φ(φ>0)个单位后为奇函数,则φ最小值是
的图象向右平移φ(φ>0)个单位后为奇函数,则φ最小值是 ![]() .
.
其中正确的结论是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆E:x2+(y﹣ ![]() )2=
)2= ![]() 经过椭圆C:
经过椭圆C: ![]() +
+ ![]() =1(a>b>0)的左右焦点F1 , F2 , 且与椭圆C在第一象限的交点为A,且F1 , E,A三点共线,直线l交椭圆C于M,N两点,且
=1(a>b>0)的左右焦点F1 , F2 , 且与椭圆C在第一象限的交点为A,且F1 , E,A三点共线,直线l交椭圆C于M,N两点,且 ![]() =λ
=λ ![]() (λ≠0)
(λ≠0) 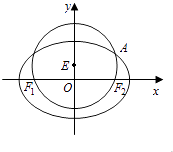
(1)求椭圆C的方程;
(2)当三角形AMN的面积取得最大值时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为锐角△ABC三个内角A,B,C的对边,且(a+b)(sinA﹣sinB)=(c﹣b)sinC (Ⅰ)求∠A的大小;
(Ⅱ)若f(x)= ![]() sin
sin ![]() cos
cos ![]() +cos2
+cos2 ![]() ,求f(B)的取值范围.
,求f(B)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C1: ![]() =1,双曲线C2:
=1,双曲线C2: ![]() =1(a>0,b>0)的左、右焦点分别为F1 , F2 , M 是双曲线C2 一条渐近线上的点,且OM⊥MF2 , 若△OMF2的面积为 16,且双曲线C1 , C2的离心率相同,则双曲线C2的实轴长为( )
=1(a>0,b>0)的左、右焦点分别为F1 , F2 , M 是双曲线C2 一条渐近线上的点,且OM⊥MF2 , 若△OMF2的面积为 16,且双曲线C1 , C2的离心率相同,则双曲线C2的实轴长为( )
A.4
B.8
C.16
D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】知函数f(x)=ax2﹣2x+lnx(a≠0,a∈R).
(1)判断函数 f (x)的单调性;
(2)若函数 f (x)有两个极值点x1 , x2 , 求证:f(x1)+f(x2)<﹣3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC 的内角 A,B,C 的对边分别是a,b,c,且 ![]() a=
a= ![]() b cosC+c sinB. (Ⅰ)求角B 的大小;
b cosC+c sinB. (Ⅰ)求角B 的大小;
(Ⅱ)若点M 为BC的中点,且 AM=AC,求sin∠BAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量 ![]() =(a,
=(a, ![]() b)与
b)与 ![]() =(cosA,sinB)平行. (Ⅰ)求A;
=(cosA,sinB)平行. (Ⅰ)求A;
(Ⅱ)若a= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com