已知实数a、b∈{-2,-1,1}
(1)求直线y=ax+b不经过第一象限的概率;
(2)求直线y=ax+b与圆x2+y2=1有公共点的概率.
解:记直线y=-2x+1为(-2,1).
由题意,实数a、b∈{-2,-1,1},
所以(a,b)共有以下9种可能结果.(-2,-2),(-2,-1),(-2,1),(-1,-2),(-1,-1),(-1,1),(1,-2),(1,-1),(1,1).每种结果是等可能的,故试验中包含9个基本事件
设事件A:“直线y=ax+b不经过第一象限”,
则它包含(-2,-2),(-2,-1),,(-1,-2),(-1,-1)四个基本事件
∴
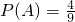
(2)设事件B:“y=ax+b与圆x
2+y
2=1有公共点”,
则可知
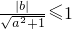
,即b
2≤a
2+1,
则它包含(-2,-2),(-2,-1),(-2,1),(-1,-1),(-1,1),(1,-1),(1,1)共7个基本事件
∴

答:直线y=ax+b不经过第一象限概率为

;y=ax+b与圆x
2+y
2=1有公共点为

.
分析:(1)列出由a,b做直线的斜率与纵截距所以的结果,列出直线y=ax+b不经过第一象限的所有的结果,利用古典概型的概率公式求出直线y=ax+b不经过第一象限的概率.
(2)利用直线与圆的位置关系的判断条件,列出直线y=ax+b与圆x
2+y
2=1有公共点转化为圆心到直线的距离大于半径得到a,b满足的不等式,列举出所有的a,b情况,利用古典概型的概率公式求出概率值.
点评:求古典概型的概率,首先要求出各个事件包含的基本事件个数,求事件的基本事件的个数的方法有:列举法、排列、组合的方法、图表法.

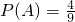
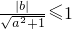 ,即b2≤a2+1,
,即b2≤a2+1,
 ;y=ax+b与圆x2+y2=1有公共点为
;y=ax+b与圆x2+y2=1有公共点为 .
.
