
【题目】已知四棱锥P—ABCD中,PA⊥平面ABCD,∠DAB=∠ADC=90°,DC=![]() AB,F,M分别是线段PC,PB的中点.
AB,F,M分别是线段PC,PB的中点.

(1)在线段AB上找出一点N,使得平面CMN∥平面PAD,并给出证明过程;
(2)若PA=![]() AB,DC=
AB,DC=![]() AD,求二面角C—AF—D的余弦值.
AD,求二面角C—AF—D的余弦值.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,然后通过中位线,证明线线平行,进而得到线面平行,进而得到面面平行.(2)以
,然后通过中位线,证明线线平行,进而得到线面平行,进而得到面面平行.(2)以![]() 分别为
分别为![]() 轴建立空间直角坐标系,通过计算平面
轴建立空间直角坐标系,通过计算平面![]() 和平面
和平面![]() 的法向量,来求得面面角的余弦值.
的法向量,来求得面面角的余弦值.
(1)证明:取AB的中点N,连接CN,MN,取PA的中点Q,连接QM,DQ;
在![]() 中,MQ
中,MQ![]() AB,
AB,![]() ,而
,而![]()
![]() ,故AB//CD,
,故AB//CD,
故QM//DC,且QM=DC,![]() 四边形CDQM为平行四边形,
四边形CDQM为平行四边形,![]() CM//DQ,
CM//DQ,
又![]() 平面PAD,
平面PAD,![]() 平面PAD,
平面PAD,![]()
![]() 平面PAD;
平面PAD;
∵MN![]() PA,
PA,![]() 平面PAD,PA
平面PAD,PA![]() 平面PAD,
平面PAD,![]() MN//平面PAD;
MN//平面PAD;
因为![]() ,故平面CMN//平面PAD;
,故平面CMN//平面PAD;
(2)由已知得:![]() 两两垂直,以
两两垂直,以![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系,设
轴建立如图所示的空间直角坐标系,设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]()
所以![]() ,
,![]() .
.
设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则
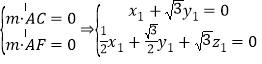 ,令
,令![]() ,得
,得![]() .
.
设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则
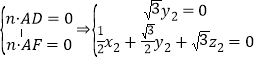 ,令
,令![]()
![]() ,
,
![]()
![]() .
.
又二面角![]() 为锐角,故二面角
为锐角,故二面角![]() 的余弦值为
的余弦值为![]() .
.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.经过任意三点有且只有一个平面.
B.过点![]() 有且仅有一条直线与异面直线
有且仅有一条直线与异面直线![]() 垂直.
垂直.
C.一条直线与一个平面平行,它就和这个平面内的任意一条直线平行.
D.面![]() 与平面
与平面![]() 相交,则公共点个数为有限个.
相交,则公共点个数为有限个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() ,且
,且![]() )是定义域为R的奇函数.
)是定义域为R的奇函数.
(1)求t的值;
(2)若![]() ,求使不等式
,求使不等式![]() 对一切
对一切![]() 恒成立的实数k的取值范围;
恒成立的实数k的取值范围;
(3)若函数![]() 的图象过点
的图象过点![]() ,是否存在正数m(
,是否存在正数m(![]() ),使函数
),使函数![]() 在
在![]() 上的最大值为0,若存在,求出m的值;若不存在,请说明理由.
上的最大值为0,若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某客户准备在家中安装一套净水系统,该系统为二级过滤,使用寿命为十年如图所示两个二级过滤器采用并联安装,再与一级过滤器串联安装.

其中每一级过滤都由核心部件滤芯来实现在使用过程中,一级滤芯和二级滤芯都需要不定期更换(每个滤芯是否需要更换相互独立).若客户在安装净水系统的同时购买滤芯,则一级滤芯每个160元,二级滤芯每个80元.若客户在使用过程中单独购买滤芯则一级滤芯每个400元,二级滤芯每个200元.现需决策安装净水系统的同时购买滤芯的数量,为此参考了根据100套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中表1是根据100个一级过滤器更换的滤芯个数制成的频数分布表,图2是根据200个二级过滤器更换的滤芯个数制成的条形图.
表1:一级滤芯更换频数分布表
一级滤芯更换的个数 | 8 | 9 |
频数 | 60 | 40 |
图2:二级滤芯更换频数条形图

以100个一级过滤器更换滤芯的频率代替1个一级过滤器更换滤芯发生的概率,以200个二级过滤器更换滤芯的频率代替1个二级过滤器更换滤芯发生的概率.
(1)求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为16的概率;
(2)记![]() 表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求
表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)记![]() 分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若
分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若![]() ,且
,且![]() ,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定
,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】山东省于2015年设立了水下考古研究中心,以此推动全省的水下考古、水下文化遗产保护等工作;水下考古研究中心工作站,分别设在位于刘公岛的中国甲午战争博物院和威海市博物馆。为对刘公岛周边海域水底情况进行详细了解,然后再选择合适的时机下水探摸、打捞,省水下考古中心在一次水下考古活动中,某一潜水员需潜水![]() 米到水底进行考古作业,其用氧量包含以下三个方面:
米到水底进行考古作业,其用氧量包含以下三个方面:
①下潜平均速度为![]() 米/分钟,每分钟的用氧量为
米/分钟,每分钟的用氧量为![]() 升;
升;
②水底作业时间范围是最少10分钟最多20分钟,每分钟用氧量为0.4升;
③返回水面时,平均速度为![]() 米/分钟,每分钟用氧量为0.32升.
米/分钟,每分钟用氧量为0.32升.
潜水员在此次考古活动中的总用氧量为![]() 升.
升.
(Ⅰ)如果水底作业时间是![]() 分钟,将
分钟,将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)若![]() ,水底作业时间为20分钟,求总用氧量
,水底作业时间为20分钟,求总用氧量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
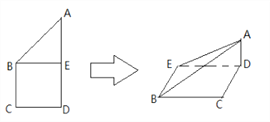
【题目】如图所示,正方形![]() 的边长为
的边长为![]() ,已知
,已知![]() ,将
,将![]() 沿
沿![]() 边折起,折起后
边折起,折起后![]() 点在平面
点在平面![]() 上的射影为
上的射影为![]() 点,则翻折后的几何体中有如下描述:①
点,则翻折后的几何体中有如下描述:①![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ;②
;②![]() ;③
;③![]() ;④平面
;④平面![]() 平面
平面![]() ,其中正确的命题序号为___________.
,其中正确的命题序号为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com