
【题目】随着创新驱动发展战略的不断深入实施,高新技术企业在科技创新和经济发展中的带动作用日益凸显,某能源科学技术开发中心拟投资开发某新型能源产品,估计能获得![]() 万元的投资收益,现准备制定一个对科研课题组的奖励议案:奖金
万元的投资收益,现准备制定一个对科研课题组的奖励议案:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,奖金不超过
(单位:万元)的增加而增加,奖金不超过![]() 万元,同时奖金不超过投资收益的
万元,同时奖金不超过投资收益的![]() .(即:设奖励方案函数模拟为
.(即:设奖励方案函数模拟为![]() 时,则公司对函数模型的基本要求是:当
时,则公司对函数模型的基本要求是:当![]() 时,①
时,①![]() 是增函数;②
是增函数;②![]() 恒成立;③
恒成立;③![]() 恒成立.)
恒成立.)
(1)现有两个奖励函数模型:(I)![]() ;(II)
;(II)![]() .试分析这两个函数模型是否符合公司要求?
.试分析这两个函数模型是否符合公司要求?
(2)已知函数![]() 符合公司奖励方案函数模型要求,求实数
符合公司奖励方案函数模型要求,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 函数(I)不符合公司要求;(II)模型符合公司要求;(2) ![]()
【解析】
(1)分别判断两个函数模型是否满足三个条件即可.
(2)由题意得函数![]() 满足三个条件,利用函数的单调性、均值不等式可求得
满足三个条件,利用函数的单调性、均值不等式可求得![]() 的取值范围.
的取值范围.
(1)对于函数模型(I):因为![]() ,即函数(I)不符合条件③,
,即函数(I)不符合条件③,
所以函数模型(I)![]() 不符合公司要求.
不符合公司要求.
对于函数模型(II):当![]() 时,
时,![]() 是增函数,
是增函数,
且![]() ,所以
,所以![]() 恒成立.
恒成立.
设![]() ,因为
,因为![]() ,
,
所以当![]() 时,
时,![]() .
.
所以![]() 恒成立.
恒成立.
所以函数模型(II)![]() 符合公司要求.
符合公司要求.
(2)因为![]() ,所以函数
,所以函数![]() 满足条件①.
满足条件①.
由函数![]() 满足条件②得:
满足条件②得:![]() ,所以
,所以![]() .
.
由函数![]() 满足条件③得:
满足条件③得:![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,因为
恒成立,因为![]() ,
,
当且仅当![]() 时等号成立,所以
时等号成立,所以![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】若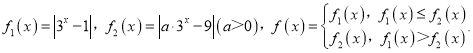
(1)当![]() 时,设
时,设![]() 所对应的自变量取值区间的长度为
所对应的自变量取值区间的长度为![]() (闭区间
(闭区间![]() 的长度为
的长度为![]() ),试求
),试求![]() 的最大值;
的最大值;
(2)是否存在这样的![]() 使得当
使得当![]() 时,
时,![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别为
分别为![]() 的三内角A,B,C的对边,其面积
的三内角A,B,C的对边,其面积![]() ,在等差数列
,在等差数列![]() 中,
中,![]() ,公差
,公差![]() .数列
.数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,如表是该地一建设银行连续五年的储蓄存款(年底余额),如表1
![]()
为了研究计算方便,工作人员将上表的数据进行了处理,令![]() ,
,![]() 得到表2:
得到表2:
![]()
(1)求:![]() 关于t的线性回归方程;
关于t的线性回归方程;
(2)通过(1)中的方程,求出y关于![]() 的回归方程;
的回归方程;
(3)用所求回归方程预测到2019年年底,该地储蓄存款额可达多少?
附:对于线性回归方程![]() ,其中
,其中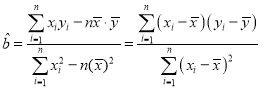 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校从参加高一年级期中考试的学生中抽出50名学生,并统计了她们的数学成绩(成绩均为整数且满分为150分),得到的样本频率分布表如下:
分组 | 频数 | 频率 |
| 2 | 0.04 |
| 3 | 0.06 |
| 14 | 0.28 |
| 15 | 0.30 |
|
|
|
| 4 | 0.08 |
合计 |
|
|
(1)在给出的样本频率分布表中,求![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)估计成绩在120分以上(含120分)学生的比例;
(3)抽取的50名学生中,为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在![]() 的学生中选两位同学,共同帮助成绩在
的学生中选两位同学,共同帮助成绩在![]() 中的某一位同学.已知甲同学的成绩为62分,乙同学的成绩为135分,求甲、乙两同学恰好被安排在同一小组的概率.
中的某一位同学.已知甲同学的成绩为62分,乙同学的成绩为135分,求甲、乙两同学恰好被安排在同一小组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 九章算术
九章算术![]() 是我国古代著名数学经典
是我国古代著名数学经典![]() 其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小
其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小![]() 以锯锯之,深一寸,锯道长一尺
以锯锯之,深一寸,锯道长一尺![]() 问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺
问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺![]() 问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示
问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示![]() 阴影部分为镶嵌在墙体内的部分
阴影部分为镶嵌在墙体内的部分![]() 已知弦
已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算该木材镶嵌在墙中的体积约为( )(注:1丈
寸,估算该木材镶嵌在墙中的体积约为( )(注:1丈![]() 尺
尺![]() 寸,
寸,![]() ,
,![]() )
)

A. 600立方寸 B. 610立方寸 C. 620立方寸 D. 633立方寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (Ⅰ)求曲线
(Ⅰ)求曲线![]() 的直角坐标方程,并指出其表示何种曲线;(Ⅱ)设直线
的直角坐标方程,并指出其表示何种曲线;(Ⅱ)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若点
两点,若点![]() 的直角坐标为
的直角坐标为![]() ,试求当
,试求当![]() 时,
时,![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如![]() ,在不超过13的素数中,随机选取两个不同的数,其和为偶数的概率是________(用分数表示)
,在不超过13的素数中,随机选取两个不同的数,其和为偶数的概率是________(用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() ,双曲线
,双曲线![]() 的左、右焦点分别为F1,F2,M是双曲线C2的一条渐近线上的点,且OM⊥MF2,O为坐标原点,若
的左、右焦点分别为F1,F2,M是双曲线C2的一条渐近线上的点,且OM⊥MF2,O为坐标原点,若![]() ,且双曲线C1,C2的离心率相同,则双曲线C2的实轴长是 ( )
,且双曲线C1,C2的离心率相同,则双曲线C2的实轴长是 ( )
A. 32 B. 4 C. 8 D. 16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com