【题目】不期而至的新冠肺炎疫情，牵动了亿万国人的心，全国各地纷纷捐赠物资驰援武汉.有一批捐赠物资需要通过轮船沿长江运送至武汉，已知该运送物资的轮船在航行中每小时的燃料费和它的速度的立方成正比，已知当速度为10海里/时时，燃料费是6元/时，而其他与速度无关的费用是96元/时，问当轮船的速度是多少时，航行1海里所需的费用总和最小？
科目：高中数学 来源： 题型：
【题目】如图，
地到火车站共有两条路径，据统计两条路径所用的时间互不影响，所用时间在各时间段内的的频率如下表：
时间（分钟） |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
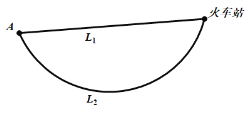
现甲、乙两人分别有
分钟和
分钟时间用于赶往火车站.
（1）为了尽最大可能在各自允许的时间内赶到火车站，甲和乙应如何选择各自的路径？
（2）用
表示甲、乙两人中在允许的时间内赶到火车站的人数，针对（1）的选择方案，求的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在研究吸烟与患肺癌的关系中，通过收集数据、整理分析数据得“吸烟与患肺癌有关”的结论，并且在犯错误的概率不超过0.01的前提下认为这个结论是成立的，下列说法中正确的是（ ）
A.100个吸烟者中至少有99人患有肺癌
B.1个人吸烟，那么这个人有99%的概率患有肺癌
C.在100个吸烟者中一定有患肺癌的人
D.在100个吸烟者中可能一个患肺癌的人也没有
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点
是椭圆C：
上的一点，椭圆C的离心率与双曲线
的离心率互为倒数，斜率为
直线l交椭圆C于B，D两点，且A、B、D三点互不重合．
（1）求椭圆C的方程；
（2）若
分别为直线AB，AD的斜率，求证：
为定值。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列选项中，说法正确的是（ ）
A.命题“
，
”的否定为“
，
”；
B.命题“在
中，
，则
”的逆否命题为真命题；
C.已知
、m是两条不同的直线，
是个平面，若
，则
；
D.已知定义在R上的函数
，则“为奇函数”是“
”的充分必要条件.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设
、
分别是椭圆
的左、右焦点.若
是该椭圆上的一个动点，
的最大值为1.
（1）求椭圆
的方程；
（2）设直线
与椭圆交于
两点，点
关于
轴的对称点为
(与
不重合)，则直线
与轴是否交于一个定点？若是，请写出定点坐标，并证明你的结论；若不是，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在极坐标系
中，
，
，
，
，
，弧
，
所在圆的圆心分别是
，
，曲线
是弧，曲线
是线段
，曲线
是线段
，曲线
是弧.
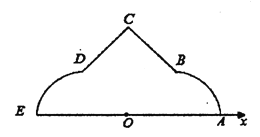
（1）分别写出，，，的极坐标方程；
（2）曲线
由，，，构成，若点
，（
），在上，则当
时，求点
的极坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：极坐标与参数方程
在极坐标系下，已知圆O：
和直线
（1）求圆O和直线l的直角坐标方程；
（2）当
时，求直线l与圆O公共点的一个极坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
