
【题目】已知数列![]() 满足
满足![]() ,其中
,其中![]() ,
,![]() 是不为1的常数.
是不为1的常数.
(Ⅰ)证明:若![]() 是递增数列,则
是递增数列,则![]() 不可能是等差数列;
不可能是等差数列;
(Ⅱ)证明:若![]() 是递减的等比数列,则
是递减的等比数列,则![]() 中的每一项都大于其后任意
中的每一项都大于其后任意![]() 个项的和;
个项的和;
(Ⅲ)若![]() ,且
,且![]() 是递增数列,
是递增数列,![]() 是递减数列,求数列
是递减数列,求数列![]() 的通项公式.
的通项公式.
【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析;(Ⅲ)![]() .
.
【解析】
试题分析:(Ⅰ)由![]() 是递增数列,则
是递增数列,则![]() ,利用反证法假设数列
,利用反证法假设数列![]() 是等差数列,得
是等差数列,得![]() ,解得
,解得![]() 或
或![]() ,可知假设不成立;(Ⅱ)由
,可知假设不成立;(Ⅱ)由![]() 是递减数列,得
是递减数列,得
![]() ,因为数列
,因为数列![]() 是等比数列,所以
是等比数列,所以![]() ,得
,得![]() ,则
,则![]() ,公比
,公比![]() ,故
,故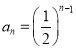 ,由于
,由于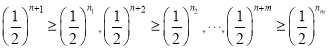 ,得
,得
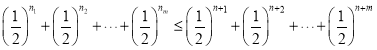 ,又
,又
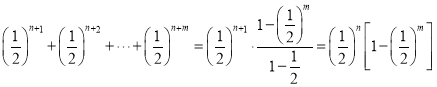 ,且
,且
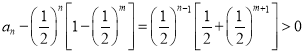 ,故
,故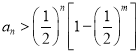 ,
,
即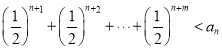 ,得证;(Ⅲ)由
,得证;(Ⅲ)由![]() 是递增数列,得
是递增数列,得![]() ,则
,则![]() ,由
,由![]() ,得
,得![]() ,所以
,所以![]() ,同理,由
,同理,由![]() 是递减数列,得
是递减数列,得![]() ,故
,故![]() ,所以
,所以![]() ,
,
累加可得![]() .
.
试题解析:(Ⅰ)因为![]() 是递增数列,所以
是递增数列,所以![]() 。
。
由于![]() ,所以
,所以![]() 。
。
假设数列![]() 是等差数列,那么
是等差数列,那么![]() 成等差数列。
成等差数列。
所以![]() ,因而
,因而![]() ,解得
,解得![]() 或
或![]() 。
。
由已知![]() ,当
,当![]() ,这与
,这与![]() 是递增数列矛盾,故
是递增数列矛盾,故![]() 的值不存在。
的值不存在。
所以数列![]() 不可能是等差数列。
不可能是等差数列。
(Ⅱ)因为![]() 是递减数列,所以
是递减数列,所以![]() 。
。
因为![]() ,所以
,所以![]() 。
。
因为数列![]() 是等比数列,
是等比数列,
所以![]() ,得
,得![]() 或
或![]() (舍去)。
(舍去)。
则![]() ,公比
,公比![]() ,故
,故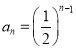 。
。
设![]() ,那么
,那么![]() 。
。
因为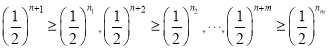 ,
,
所以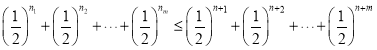 。
。
因为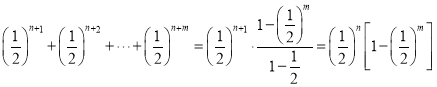
而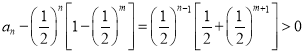 ,即
,即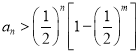 ,
,
所以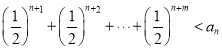 。
。
即:数列![]() 中的每一项大于其后任意
中的每一项大于其后任意![]() 个项的和。
个项的和。
(Ⅲ)由于![]() 是递增数列,所以
是递增数列,所以![]() ,
,
所以![]() 。 ①
。 ①
因为![]() ,所以
,所以![]() 。 ②
。 ②
由①②知,![]() ,因此
,因此![]() 。 ③
。 ③
因为![]() 是递减数列,同理,
是递减数列,同理,![]() ,
,
故![]() 。 ④
。 ④
由③④可知,![]() 。
。
因此![]()
![]()
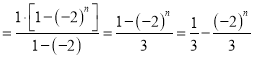 。
。
所以数列![]() 的通项公式为
的通项公式为![]() 。
。


科目:高中数学 来源: 题型:
【题目】已知![]() 是一元二次方程
是一元二次方程![]() 的两个实数根.
的两个实数根.
(1)是否存在实数![]() ,使
,使![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(2)求使![]() 的值为整数的实数
的值为整数的实数![]() 的整数值.
的整数值.
(3)已知对于x的所有实数值,二次函数![]() 的值都是非负的,求关于x的方程
的值都是非负的,求关于x的方程![]() 的根的取值范围
的根的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆心在直线x﹣y+2=0上,且与两坐标轴都相切的圆的方程为( )
A. (x+1)2+(y﹣1)2=1 B. (x﹣1)2+(y+1)2=1 C. (x﹣1)2+(y+1)2=2 D. (x﹣1)2+(y﹣1)2=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(1)写出价格![]() 关于时间
关于时间![]() 的函数关系式;(
的函数关系式;(![]() 表示投放市场的第
表示投放市场的第![]() 天);
天);
(2)销售量![]() 与时间
与时间![]() 的函数关系:
的函数关系:![]() ,则该产品投放市场第几天销售额最高?最高为多少千元?
,则该产品投放市场第几天销售额最高?最高为多少千元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,函数
上单调递增,函数 .
.
(1)请写出函数![]() 与函数
与函数![]() 在
在![]() 的单调区间(只写结论,不证明);
的单调区间(只写结论,不证明);
(2)求函数![]() 的最值;
的最值;
(3)讨论方程![]() 实根的个数.
实根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下给出对程序框图的几种说法:
①任何一个程序框图都必须有起止框;②输入框只能紧接开始框,输出框只能紧接结束框;③判断框是唯一具有超出一个退出点的符号;④对于一个问题的算法来说,其程序框图判断框内的条件的表述方法是唯一的.
其中正确说法的个数是__________个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量ξ+η=8,若ξ~B(10,0.6),则E(η),D(η)分别是 ( )
A. 6和2.4 B. 2和2.4
C. 2和5.6 D. 6和5.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com