
【题目】已知![]() 是一元二次方程
是一元二次方程![]() 的两个实数根.
的两个实数根.
(1)是否存在实数![]() ,使
,使![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(2)求使![]() 的值为整数的实数
的值为整数的实数![]() 的整数值.
的整数值.
(3)已知对于x的所有实数值,二次函数![]() 的值都是非负的,求关于x的方程
的值都是非负的,求关于x的方程![]() 的根的取值范围
的根的取值范围
【答案】(1)不存在实数![]() (2)
(2)![]() (3)
(3)![]()
【解析】
试题分析:(1)根据已知方程有两个实数根,那么△≥0,可得k的范围,由于方程有两个实数根,那么根据根与系数的关系可得![]() ,然后把
,然后把![]() 代入
代入![]() 中,进而可求k的值;(2)由
中,进而可求k的值;(2)由![]() 是一元二次方程4kx2-4kx+k+2=0的两个实数根,利用根与系数的关系表示出
是一元二次方程4kx2-4kx+k+2=0的两个实数根,利用根与系数的关系表示出![]() ,将
,将![]() 通分并利用同分母分式的加法法则计算,利用完全平方公式变形后,把表示出
通分并利用同分母分式的加法法则计算,利用完全平方公式变形后,把表示出![]() 代入,整理后根据此式子的值为整数,即可求出实数k的整数值;(3)先根据
代入,整理后根据此式子的值为整数,即可求出实数k的整数值;(3)先根据![]() 的值都是非负的,判别式小于等于0求得a的范围,进而根据a的范围确定函数x的解析式,根据函数的单调性求得函数的值域
的值都是非负的,判别式小于等于0求得a的范围,进而根据a的范围确定函数x的解析式,根据函数的单调性求得函数的值域
试题解析:(1)假设存在实数![]() ,使
,使![]() 成立.
成立.
∵ 一元二次方程![]() 的两个实数根
的两个实数根
∴  ,
,
又![]() 是一元二次方程
是一元二次方程![]() 的两个实数根
的两个实数根
∴ 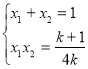
∴![]()
![]() ,但
,但![]() .
.
∴不存在实数![]() ,使
,使![]() 成立.
成立.
(2)∵ ![]()
∴ 要使其值是整数,只需![]() 能被4整除,故
能被4整除,故![]() ,注意到
,注意到![]() ,
,
故要使![]() 的值为整数的实数
的值为整数的实数![]() 的整数值为
的整数值为![]() .
.
(3)![]() 的图像开口向上
的图像开口向上
要![]() 的值都是非负
的值都是非负
即![]()
![]() -
-
①当![]() 时
时
![]()
![]()
![]()
![]()
当![]() 时
时
![]() 的最大值等于
的最大值等于![]()
当![]() 时
时
![]() 的最小值等于
的最小值等于![]()
②当![]() 时
时
![]()
![]()
![]() =
=
当![]() 时
时
![]() 的最小值等于6
的最小值等于6
当![]() 时
时
![]() 的最大值等于12
的最大值等于12
综上所述,![]() 的取值范围是
的取值范围是![]() 。
。


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】用系统抽样法(按等距离的规则)从160名学生中抽取容量为20的样本,将这160名学生从1到160编号.按编号顺序平均分成20段(1~8号,9~16号,…,153~160号),若第16段应抽出的号码为125,则第1段中用简单随机抽样确定的号码是( )
A.7
B.5
C.4
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为1的等边三角形![]() 中,
中,![]() 分别是
分别是![]() 边上的点,
边上的点,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 与
与![]() 交于点
交于点![]() ,将
,将![]() 沿
沿![]() 折起,得到如图2所示的三棱锥
折起,得到如图2所示的三棱锥![]() ,其中
,其中![]() .
.
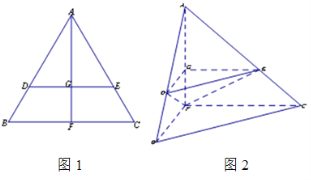
(1) 证明:![]() //平面
//平面![]() ;
;
(2) 证明:![]()
![]() 平面
平面![]() ;
;
(3) 当![]() 时,求三棱锥
时,求三棱锥![]() 的体积
的体积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰梯形![]() 中,
中,![]() ,
,![]() 为
为![]() 中点, 点
中点, 点![]() 分别为
分别为![]() 的中点, 将
的中点, 将![]() 沿
沿![]() 折起到
折起到 ![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() (如图
(如图 ![]() ).
).


(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)侧棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,其中
,其中![]() ,
,![]() 是不为1的常数.
是不为1的常数.
(Ⅰ)证明:若![]() 是递增数列,则
是递增数列,则![]() 不可能是等差数列;
不可能是等差数列;
(Ⅱ)证明:若![]() 是递减的等比数列,则
是递减的等比数列,则![]() 中的每一项都大于其后任意
中的每一项都大于其后任意![]() 个项的和;
个项的和;
(Ⅲ)若![]() ,且
,且![]() 是递增数列,
是递增数列,![]() 是递减数列,求数列
是递减数列,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列问题中是古典概型的是( )
A.种下一粒杨树种子,求其能长成大树的概率
B.掷一颗质地不均匀的骰子,求出现1点的概率
C.在区间[1,4]上任取一数,求这个数大于1.5的概率
D.同时掷两枚质地均匀的骰子,求向上的点数之和是5的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com