
【题目】已知函数![]() .
.
若曲线![]() 在
在![]() 处的切线斜率为0,求a的值;
处的切线斜率为0,求a的值;
(Ⅱ)若![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(Ⅲ)求证:当![]() 时,曲线
时,曲线![]() (x>0)总在曲线
(x>0)总在曲线![]() 的上方.
的上方.
【答案】(I)![]() . (II)
. (II)![]() .(III)见解析.
.(III)见解析.
【解析】试题分析:(Ⅰ)利用导函数在x=0处的值等于零,可以求出a的值.
(Ⅱ)![]() .分
.分![]() ,
,![]() ,
,![]() 三种情况讨论求
三种情况讨论求![]() 的最小值即可;
的最小值即可;
(Ⅲ) 当![]() 时,构造
时,构造![]() ,证明
,证明![]()
试题解析:(I)函数![]() 的定义域为
的定义域为![]() .
.
因为![]() ,所以
,所以![]() .
.
由![]() 得
得![]() .
.
(II)![]() .
.
①当![]() 时,令
时,令![]() 得
得![]() .
.
![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以当![]() 时,
时,![]() 有最小值
有最小值![]() .
.
“![]() 恒成立”等价于“
恒成立”等价于“![]() 最小值大于等于0”,即
最小值大于等于0”,即![]() .
.
因为![]() ,所以
,所以![]() .
.
②当![]() 时,
时,![]() 符合题意;
符合题意;
③当![]() 时,取
时,取![]() ,则
,则![]() ,不符合题意.
,不符合题意.
综上,若![]() 对
对![]() 恒成立,则
恒成立,则![]() 的取值范围为
的取值范围为![]() .
.
(III)当![]() 时,令
时,令![]() ,可求
,可求![]() .
.
因为![]() ,
,![]() ,且
,且![]() 在
在![]() 上单调递增,
上单调递增,
所以在(0,![]() )上存在唯一的
)上存在唯一的![]() ,使得
,使得![]() ,即
,即![]() ,且
,且
![]() .
.
当![]() 变化时,
变化时,![]() 与
与![]() 在(0,
在(0,![]() )上的情况如下:
)上的情况如下:
|
|
|
|
|
| 0 |
|
|
| 极小 |
|
则当![]() 时,
时,![]() 存在最小值
存在最小值![]() ,且
,且![]() .
.
因为![]() ,所以
,所以![]() .
.
所以当![]() 时,
时,![]()
所以当![]() 时,曲线
时,曲线![]() 总在曲线
总在曲线![]() 的上方.
的上方.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】对于![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() 与⑥
与⑥![]() ,选择恰当的关系式序号填空:
,选择恰当的关系式序号填空:
(1)角![]() 为第一象限角的充要条件是_____;
为第一象限角的充要条件是_____;
(2)角![]() 为第二象限角的充要条件是_____;
为第二象限角的充要条件是_____;
(3)角![]() 为第三象限角的充要条件是_____;
为第三象限角的充要条件是_____;
(4)角![]() 为第四象限角的充要条件是______.
为第四象限角的充要条件是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() 的前n项和为
的前n项和为![]() ,记
,记![]() ,
, ![]() ,…,
,…, ![]() 中奇数的个数为
中奇数的个数为![]() .
.
(Ⅰ)若![]() = n,请写出数列
= n,请写出数列![]() 的前5项;
的前5项;
(Ⅱ)求证:"![]() 为奇数,
为奇数, ![]() (i = 2,3,4,...)为偶数”是“数列
(i = 2,3,4,...)为偶数”是“数列![]() 是单调递增数列”的充分不必要条件;
是单调递增数列”的充分不必要条件;
(Ⅲ)若![]() ,i=1, 2, 3,…,求数列
,i=1, 2, 3,…,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用适当的方法表示下列集合:
(1)一年中有31天的月份的全体;
(2)大于![]() 小于12.8的整数的全体;
小于12.8的整数的全体;
(3)梯形的全体构成的集合;
(4)所有能被3整除的数的集合;
(5)方程![]() 的解组成的集合;
的解组成的集合;
(6)不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,EB垂直于菱形ABCD所在平面,且EB=BC=2,∠BAD=60°,点G、H分别为边CD、DA的中点,点M是线段BE上的动点.
(I)求证:GH⊥DM;
(II)当三棱锥D-MGH的体积最大时,求点A到面MGH的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲:82,81,79,78,95,88,93,84;乙:92,95,80,75,83,80,90,85
(1) 用茎叶图表示这两组数据,并计算平均数与方差;
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中两个)考虑,你认为选派哪位学生参加合适?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
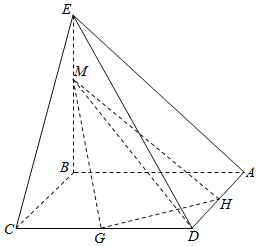
【题目】如图,在边长为![]() 的菱形
的菱形![]() 中,
中,![]() .点
.点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,点
上,点![]() 与点
与点![]() ,
,![]() 不重合,
不重合,![]() ,
,![]() .沿
.沿![]() 将
将![]() 翻折到
翻折到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)当![]() 与平面
与平面![]() 所成的角为
所成的角为![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com