
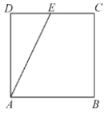
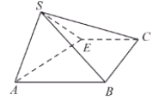
【题目】如图,点![]() 为正方形
为正方形![]() 边
边![]() 上异于点
上异于点![]() ,
,![]() 的动点,将
的动点,将![]() 沿
沿![]() 翻折成
翻折成![]() ,在翻折过程中,下列说法正确的是( )
,在翻折过程中,下列说法正确的是( )
A.存在点![]() 和某一翻折位置,使得
和某一翻折位置,使得![]()
B.存在点![]() 和某一翻折位置,使得
和某一翻折位置,使得![]() 平面
平面![]()
C.存在点![]() 和某一翻折位置,使得直线
和某一翻折位置,使得直线![]() 与平面
与平面![]() 所成的角为45°
所成的角为45°
D.存在点![]() 和某一翻折位置,使得二面角
和某一翻折位置,使得二面角![]() 的大小为60°
的大小为60°
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() 、
、![]() ,其短轴的两个端点分别为
,其短轴的两个端点分别为![]() ,
,![]() ,若
,若![]() ;是边长为2的等边三角形.
;是边长为2的等边三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且斜率为
且斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
,![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得直线
,使得直线![]() ,
,![]() 的斜率乘积为定值,若存在,求出定点,若不存在,请说明理由.
的斜率乘积为定值,若存在,求出定点,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象与函数
的图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称,则关于函数
对称,则关于函数![]() 以下说法正确的是( )
以下说法正确的是( )
A. 最大值为1,图象关于直线![]() 对称B. 在
对称B. 在![]() 上单调递减,为奇函数
上单调递减,为奇函数
C. 在![]() 上单调递增,为偶函数D. 周期为
上单调递增,为偶函数D. 周期为![]() ,图象关于点
,图象关于点![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
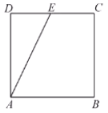
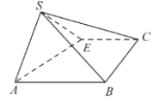
【题目】如图,点![]() 为正方形
为正方形![]() 边
边![]() 上异于点
上异于点![]() ,
,![]() 的动点,将
的动点,将![]() 沿
沿![]() 翻折成
翻折成![]() ,在翻折过程中,下列说法正确的是( )
,在翻折过程中,下列说法正确的是( )
A.存在点![]() 和某一翻折位置,使得
和某一翻折位置,使得![]()
B.存在点![]() 和某一翻折位置,使得
和某一翻折位置,使得![]() 平面
平面![]()
C.存在点![]() 和某一翻折位置,使得直线
和某一翻折位置,使得直线![]() 与平面
与平面![]() 所成的角为45°
所成的角为45°
D.存在点![]() 和某一翻折位置,使得二面角
和某一翻折位置,使得二面角![]() 的大小为60°
的大小为60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知![]() 为椭圆
为椭圆![]() 的上顶点,P为椭圆E上异于上、下顶点的一个动点.当点P的横坐标为
的上顶点,P为椭圆E上异于上、下顶点的一个动点.当点P的横坐标为![]() 时,
时,![]() .
.
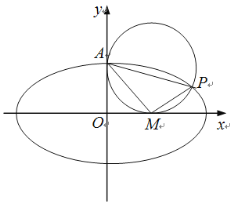
(1)求椭圆E的标准方程;
(2)设M为x轴的正半轴上的一个动点.
①若点P在第一象限内,且以AP为直径的圆恰好与x轴相切于点M,求AP的长.
②若![]() ,是否存在点N,满足
,是否存在点N,满足![]() ,且AN的中点恰好在椭圆E上?若存在,求点N的坐标;若不存在,请说明理由.
,且AN的中点恰好在椭圆E上?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秉承“绿水青山就是金山银山”的发展理念,某市环保部门通过制定评分标准,先对本市的企业进行评估,评出四个等级,并根据等级给予相应的奖惩,如下表所示:
评估得分 |
|
|
|
|
评定等级 | 不合格 | 合格 | 良好 | 优秀 |
奖励(万元) |
|
|
|
|
环保部门对企业评估完成后,随机抽取了![]() 家企业的评估得分(
家企业的评估得分(![]() 分)为样本,得到如下频率分布表:
分)为样本,得到如下频率分布表:
评估得分 |
|
|
|
|
|
|
频率 |
|
|
|
|
|
|
其中![]() 、
、![]() 表示模糊不清的两个数字,但知道样本评估得分的平均数是
表示模糊不清的两个数字,但知道样本评估得分的平均数是![]() .
.
(1)现从样本外的数百个企业评估得分中随机抽取![]() 个,若以样本中频率为概率,求该家企业的奖励不少于
个,若以样本中频率为概率,求该家企业的奖励不少于![]() 万元的概率;
万元的概率;
(2)现从样本“不合格”、“合格”、“良好”三个等级中,按分层抽样的方法抽取![]() 家企业,再从这
家企业,再从这![]() 家企业随机抽取
家企业随机抽取![]() 家,求这两家企业所获奖励之和不少于
家,求这两家企业所获奖励之和不少于![]() 万元的概率.
万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(0<p<8)的焦点为F点Q是抛物线C上的一点,且点Q的纵坐标为4,点Q到焦点的距离为5.
(1)求抛物线C的方程;
(2)设直线l不经过Q点且与抛物线交于A,B两点,QA,QB的斜率分别为K1,K2,若K1K2=﹣2,求证:直线AB过定点,并求出此定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com