
【题目】已知抛物线C:y2=2px(0<p<8)的焦点为F点Q是抛物线C上的一点,且点Q的纵坐标为4,点Q到焦点的距离为5.
(1)求抛物线C的方程;
(2)设直线l不经过Q点且与抛物线交于A,B两点,QA,QB的斜率分别为K1,K2,若K1K2=﹣2,求证:直线AB过定点,并求出此定点.
【答案】(1)y2=4x;(2)见解析,定点(6,﹣4)
【解析】
(1)由抛物线的性质到焦点的距离等于到准线的距离,设![]() 的坐标,由题意可得
的坐标,由题意可得![]() 的值,进而求出抛物线的方程;
的值,进而求出抛物线的方程;
(2)设直线![]() 的方程与抛物线联立,求出两根之和及两根之积,进而求出直线
的方程与抛物线联立,求出两根之和及两根之积,进而求出直线![]() ,
,![]() 的斜率之积,由题意可得参数之间的关系,进而求出直线
的斜率之积,由题意可得参数之间的关系,进而求出直线![]() 恒过的定点,注意直线不过
恒过的定点,注意直线不过![]() ,所以求出符合题意的定点的坐标.
,所以求出符合题意的定点的坐标.
解:(1)由题意![]() ,
,![]() ,直线方程为
,直线方程为![]() ,由抛物线的性质,到焦点的距离等于到准线的距离,
,由抛物线的性质,到焦点的距离等于到准线的距离,
由题意可得![]() ,解得
,解得![]() 或8,由题意可得
或8,由题意可得![]() ,
,
所以抛物线的方程为:![]() ;
;
(2)由题意设直线![]() 的方程为:
的方程为:![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
联立直线![]() 与抛物线的方程可得
与抛物线的方程可得![]() ,整理可得
,整理可得![]() ,
,
则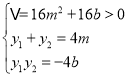 ,①
,①
由(1)可得![]() 可得
可得![]() ,
,
即![]() ,
,
即![]() ,
,
整理可得![]() ,
,
将①代入可得:![]() ,即
,即![]() ,
,
所以![]() ,或
,或![]() ,
,
即![]() ,或
,或![]() ,
,
所以直线![]() 的方程为:
的方程为:![]() ,即
,即![]() 恒过
恒过![]() ,
,
或者![]() 即
即![]() 恒过
恒过![]() ,
,
而由题意可得直线![]() 不过
不过![]() ,
,
可证得直线![]() 恒过定点
恒过定点![]() .
.



 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:
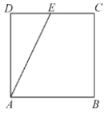
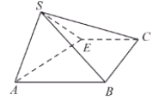
【题目】如图,点![]() 为正方形
为正方形![]() 边
边![]() 上异于点
上异于点![]() ,
,![]() 的动点,将
的动点,将![]() 沿
沿![]() 翻折成
翻折成![]() ,在翻折过程中,下列说法正确的是( )
,在翻折过程中,下列说法正确的是( )
A.存在点![]() 和某一翻折位置,使得
和某一翻折位置,使得![]()
B.存在点![]() 和某一翻折位置,使得
和某一翻折位置,使得![]() 平面
平面![]()
C.存在点![]() 和某一翻折位置,使得直线
和某一翻折位置,使得直线![]() 与平面
与平面![]() 所成的角为45°
所成的角为45°
D.存在点![]() 和某一翻折位置,使得二面角
和某一翻折位置,使得二面角![]() 的大小为60°
的大小为60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某总公司在A,B两地分别有甲、乙两个下属公司同种新能源产品(这两个公司每天都固定生产50件产品),所生产的产品均在本地销售.产品进人市场之前需要对产品进行性能检测,得分低于80分的定为次品,需要返厂再加工;得分不低于80分的定为正品,可以进人市场.检测员统计了甲、乙两个下属公司100天的生产情况及每件产品盈利亏损情况,数据如表所示:
表1
甲公司 | 得分 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
件数 | 10 | 10 | 40 | 40 | 50 | |
天数 | 10 | 10 | 10 | 10 | 80 |
表2
甲公司 | 得分 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
件数 | 10 | 5 | 40 | 45 | 50 | |
天数 | 20 | 10 | 20 | 10 | 70 |
表3
每件正品 | 每件次品 | |
甲公司 | 盈2万元 | 亏3万元 |
乙公司 | 盈3万元 | 亏3.5万元 |
(1)分别求甲、乙两个公司这100天生产的产品的正品率(用百分数表示).
(2)试问甲、乙两个公司这100天生产的产品的总利润哪个更大?说明理由.
(3)若以甲公司这100天中每天产品利润总和对应的频率作为概率,从甲公司这100天随机抽取1天,记这天产品利润总和为X,求X的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知项数为![]() 的数列
的数列![]() 满足如下条件:①
满足如下条件:①![]() ;②
;②![]() 若数列
若数列![]() 满足
满足![]() 其中
其中![]() 则称
则称![]() 为
为![]() 的“伴随数列”.
的“伴随数列”.
(I)数列![]() 是否存在“伴随数列”,若存在,写出其“伴随数列”;若不存在,请说明理由;
是否存在“伴随数列”,若存在,写出其“伴随数列”;若不存在,请说明理由;
(II)若![]() 为
为![]() 的“伴随数列”,证明:
的“伴随数列”,证明:![]() ;
;
(III)已知数列![]() 存在“伴随数列”
存在“伴随数列”![]() 且
且![]() 求
求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中已知椭圆![]() ,焦点在x轴上的椭圆
,焦点在x轴上的椭圆![]() 与
与![]() 的离心率相同,且椭圆
的离心率相同,且椭圆![]() 的外切矩形ABCD(两组对边分别平行于x轴、y轴)的顶点在椭圆
的外切矩形ABCD(两组对边分别平行于x轴、y轴)的顶点在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)设![]() 为椭圆
为椭圆![]() 上一点(不与点A、B、C、D重合).
上一点(不与点A、B、C、D重合).
①若直线:![]() ,求证:直线l与椭圆
,求证:直线l与椭圆![]() 相交;
相交;
②记①中的直线l与椭圆C1的交点为S、T,求证![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人投篮的命中率各不相同,其中乙的命中率是甲的2倍,丙的命中率等于甲与乙的命中率之和.若甲与乙各投篮一次,每人投篮相互独立,则他们都命中的概率为0.18.
(1)求甲、乙、丙三人投篮的命中率;
(2)现要求甲、乙、丙三人各投篮一次,假设每人投篮相互独立,记三人命中总次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十五巧板,又称益智图,为清朝浙江省德清知县童叶庚在同治年间所发明,它能拼出草木、花果、鸟兽、鱼虫、文字等图案.十五巧板由十五块板组成一个大正方形(如图1),其中标号为![]() 的小板为等腰直角三角形,图
的小板为等腰直角三角形,图![]() 是用十五巧板拼出的2019年生肖猪的图案,则从生肖猪图案中任取一点,该点恰好取自阴影部分的概率为( )
是用十五巧板拼出的2019年生肖猪的图案,则从生肖猪图案中任取一点,该点恰好取自阴影部分的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
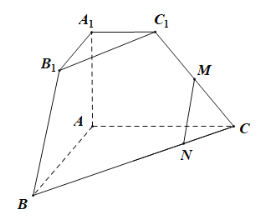
【题目】如图,在三棱台![]() 中,
中,![]() ,.若点
,.若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 靠近点
靠近点![]() 的四等分点.
的四等分点.
(1)求证:![]() 平面
平面![]() ;
;
(2)若三棱台![]() 的体积为
的体积为![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
注:台体体积公式:![]() ,或在
,或在![]() 分别为台体上下底面积,
分别为台体上下底面积,![]() 为台体的高.
为台体的高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com