
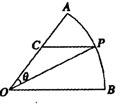
如图所示,扇形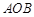 ,圆心角
,圆心角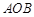 的大小等于
的大小等于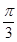 ,半径为2,在半径
,半径为2,在半径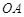 上有一动点
上有一动点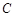 ,过点
,过点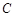 作平行于
作平行于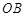 的直线交弧
的直线交弧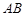 于点
于点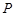 .
.
(1)若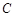 是半径
是半径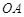 的中点,求线段
的中点,求线段 的长;
的长;
(2)设 ,求
,求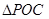 面积的最大值及此时
面积的最大值及此时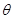 的值.
的值.
(1)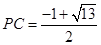 ;(2)当
;(2)当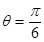 时,
时,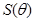 取得最大值
取得最大值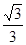 .
.
解析试题分析:(1)由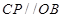 得出
得出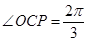 ,在
,在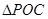 中,利用余弦定理计算
中,利用余弦定理计算 长度;(2)要求
长度;(2)要求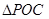 面积的最大值,需要将面积表示为
面积的最大值,需要将面积表示为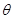 的函数再求最值,显然可以用正弦的面积公式,注意到
的函数再求最值,显然可以用正弦的面积公式,注意到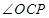 已知,故不妨用
已知,故不妨用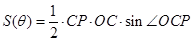 ,接下来分别把
,接下来分别把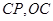 表示成
表示成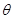 的函数,在
的函数,在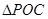 中利用正弦定理
中利用正弦定理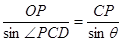 得
得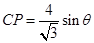 ,同理,利用正弦定理
,同理,利用正弦定理 ,得
,得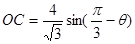 ,故
,故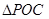 的面积
的面积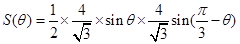 ,运用两角差的正弦公式,降幂公式以及辅助角公式将
,运用两角差的正弦公式,降幂公式以及辅助角公式将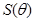 化为同角三角函数,得
化为同角三角函数,得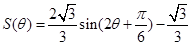 ,注意
,注意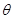 的范围是
的范围是 ,可得
,可得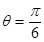 时
时 取最大值1,此时
取最大值1,此时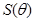 取最大值
取最大值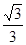 .
.
试题解析:(1)在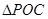 中,
中,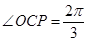 ,
, ,由
,由
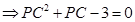
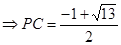 ; 5分
; 5分
(2) 平行于
平行于
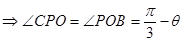 ,
,
在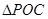 中,由正弦定理得
中,由正弦定理得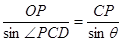 ,即
,即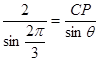 ,
, 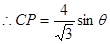 ,
,
又 ,
,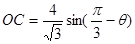 . 8分
. 8分
记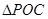 的面积为
的面积为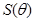 ,则
,则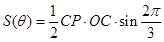
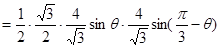

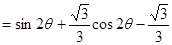
=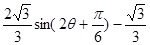 , 10分
, 10分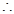 当
当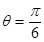 时,
时,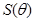 取得最大值
取得最大值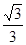 . 12分
. 12分
考点:1、三角恒等变换;2、三角函数的基本运算;3、正、余弦定理.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:解答题
若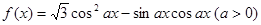 的图像与直线
的图像与直线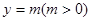 相切,并且切点横坐标依次成公差为
相切,并且切点横坐标依次成公差为 的等差数列.
的等差数列.
(1)求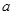 和
和 的值;
的值;
(2)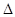 ABC中a、b、c分别是∠A、∠B、∠C的对边.若
ABC中a、b、c分别是∠A、∠B、∠C的对边.若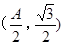 是函数
是函数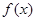 图象的一个对称中心,且a=4,求
图象的一个对称中心,且a=4,求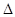 ABC面积的最大值.
ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/时的航行速度匀速行驶,经过t小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值;
(3)是否存在v,使得小艇以v海里/时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定v的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com