
【题目】已知点![]() ,点
,点![]() 是圆
是圆![]() 上的任意一点,,线段
上的任意一点,,线段![]() 的垂直平分线与直线
的垂直平分线与直线![]() 交于点
交于点![]() .
.
(1)求![]() 点的轨迹方程;
点的轨迹方程;
(2)若直线![]() 与点
与点![]() 的轨迹相切,且与圆
的轨迹相切,且与圆![]() 相交于点
相交于点![]() 和
和![]() ,求直线
,求直线![]() 和三角形
和三角形![]() 的面积.
的面积.
【答案】(1) ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据已知,由平面几何知识可得![]() ,所以E的轨迹是以点A,C为焦点的椭圆,从而可得轨迹方程;(2)由
,所以E的轨迹是以点A,C为焦点的椭圆,从而可得轨迹方程;(2)由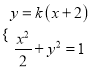 ,
,
得![]() ,根据判别式为零可得直线斜率,从而可得直线方程,再利用点到直线距离公式与三角形面积公式可得结果.
,根据判别式为零可得直线斜率,从而可得直线方程,再利用点到直线距离公式与三角形面积公式可得结果.
试题解析:(1)由题意可知![]()
![]()
![]() E的轨迹是以点A,C为焦点的椭圆
E的轨迹是以点A,C为焦点的椭圆![]()
所以椭圆的方程![]() .
.
(2)由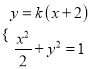 ,
,
得![]()
又![]()
![]() 与点
与点![]() 的轨迹相切
的轨迹相切
![]()
![]() 即
即![]() , 又
, 又![]() ,所以
,所以![]() ,
, ![]() 的方程
的方程![]()
![]() 圆心C到
圆心C到![]() 的距离
的距离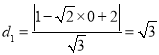 由垂径定理可知,
由垂径定理可知, ![]()
又![]() 原点O到直线
原点O到直线![]() 的距离
的距离![]()
![]()
![]() .
.
【方法点晴】本题主要考查定义法求轨迹方程、点到直线的距离公式及三角形面积公式,属于难题.求轨迹方程的常见方法有:①直接法,设出动点的坐标![]() ,根据题意列出关于
,根据题意列出关于![]() 的等式即可;②定义法,根据题意动点符合已知曲线的定义,直接求出方程;③参数法,把
的等式即可;②定义法,根据题意动点符合已知曲线的定义,直接求出方程;③参数法,把![]() 分别用第三个变量表示,消去参数即可;④逆代法,将
分别用第三个变量表示,消去参数即可;④逆代法,将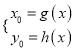 代入
代入![]() .本题(1)就是利用方法②求得
.本题(1)就是利用方法②求得![]() 的轨迹方程的.
的轨迹方程的.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】某畜牧站为了考查某种新型药物预防动物疾病的效果,利用小白鼠进行试验,得到如下丢失数据的![]() 列联表
列联表
患病 | 未患病 | 总计 | |
没服用药 | 20 | 30 | 50 |
服用药 |
|
| 50 |
总计 |
|
| 100 |
设从没服用药的小白鼠中任取两只,未患病的动物数为![]() ,从服用药物的小白鼠中任取两只,未患病的动物数为
,从服用药物的小白鼠中任取两只,未患病的动物数为![]() ,得到如下比例关系:
,得到如下比例关系:![]()
(1)求出![]() 列联表中数据
列联表中数据![]() ,
,![]() ,
,![]() ,
,![]() 的值
的值
(2)是否有![]() 的把握认为药物有效?并说明理由
的把握认为药物有效?并说明理由
(参考公式:![]() ,当
,当![]() 时,有
时,有![]() 的把握认为A与B有关;
的把握认为A与B有关;![]() 时,有
时,有![]() 的把握认为A与B有关.
的把握认为A与B有关.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每年每次租时间不超过两小时免费,超过两个小时的部分每小时收费2元(不足1小时的部分按1小时计算).现有甲、乙两人独立来该租车点租车骑游(各租一车一次).设甲、乙不超过两小时还车的概率分别为![]() ,
, ![]() ;两小时以上且不超过三小时还车的概率为
;两小时以上且不超过三小时还车的概率为![]() ,
, ![]() ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.
(1)求甲、乙都在三到四小时内还车的概率和甲、乙两人所付租车费相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
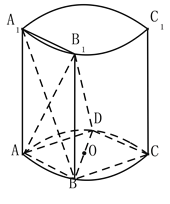
【题目】如图,在圆柱中,A,B,C,D是底面圆的四等分点,O是圆心,A1A,B1B,C1C与底面ABCD垂直,底面圆的直径等于圆柱的高.
(Ⅰ)证明:BC⊥AB1;
(Ⅱ)(ⅰ)求二面角A1 - BB1 - D的大小;
(ⅱ)求异面直线AB1和BD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2|x﹣a|(a∈R).
(1)若函数f(x)为偶函数,求a的值;
(2)当a>0时,若对任意的x∈[0,+∞),不等式f(x﹣1)≤2f(x)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系xOy中,曲线C1的参数方程为![]() (t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:
(t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2: ![]() .
.
(Ⅰ)求曲线C1和C2的直角坐标方程,并分别指出其曲线类型;
(Ⅱ)试判断:曲线C1和C2是否有公共点?如果有,说明公共点的个数;如果没有,请说明理由;
(Ⅲ)设![]() 是曲线C1上任意一点,请直接写出a + 2b的取值范围.
是曲线C1上任意一点,请直接写出a + 2b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5组,制成如图所示频率分直方图.
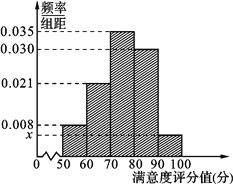
(Ⅰ) 求图中![]() 的值;
的值;
(Ⅱ) 已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取2人进行座谈,求所抽取的两人中至少有一名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查“五一”小长假出游选择“有水的地方”是否与性别有关,现从该市“五一”出游旅客中随机抽取500人进行调查,得到如下2×2列联表:(单位:人)
选择“有水的地方” | 不选择“有水的地方” | 合计 | |
男 | 90 | 110 | 200 |
女 | 210 | 90 | 300 |
合计 | 300 | 200 | 500 |
(Ⅰ)据此样本,有多大的把握认为选择“有水的地方”与性别有关;
(Ⅱ)若以样本中各事件的频率作为概率估计全市“五一”所有出游旅客情况,现从该市的全体出游旅客(人数众多)中随机抽取3人,设3人中选择“有水的地方”的人数为随机变量X,求随机变量X的数学期望和方差.
附临界值表及参考公式:
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
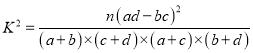 ,n=a+b+c+d.
,n=a+b+c+d.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com