
【题目】某校从高三年级期末考试的学生中抽出60名学生,其成绩(均为整数)的频率分布直方图如图所示:
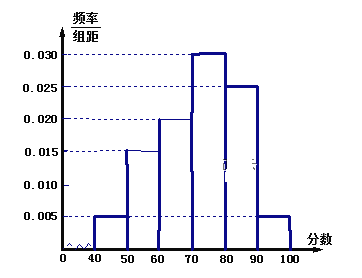
(1)估计这次考试的及格率(60分及以上为及格)和平均分;
(2)按分层抽样从成绩是80分以上(包括80分)的学生中选取6人,再从这6人中选取两人作为代表参加交流活动,求他们在不同分数段的概率.
【答案】(1)及格率是80%;平均分是![]() 分(2)
分(2)![]()
【解析】
(1)由频率分布直方图直接可计算得及格率以及平均分;
(2)按分层抽样知![]() 5人A,B,C,D,E,
5人A,B,C,D,E,![]() ”1人F,写出基本事件,事件“不同分数段”所包含的基本事件数5种,利用古典概型即可得到结论.
”1人F,写出基本事件,事件“不同分数段”所包含的基本事件数5种,利用古典概型即可得到结论.
(1)依题意,60及以上的分数所在的第三、四、五、六组,频率和为![]() ,所以抽样学生成绩的合格率是80%.-
,所以抽样学生成绩的合格率是80%.-
利用组中值估算抽样学生的平均分:
![]()
![]()
![]() .
.
估计这次考试的平均分是![]() 分
分
(2)按分层抽样抽取![]() 5人A,B,C,D,E,
5人A,B,C,D,E,![]() ”1人F.,则基本事件(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15种,事件“不同分数段”所包含的基本事件数5种,
”1人F.,则基本事件(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15种,事件“不同分数段”所包含的基本事件数5种,
故所求概率为:![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数![]() ,
, ![]() (
(![]() ).
).
(1)当![]() 时,若函数
时,若函数![]() 与
与![]() 的图象在
的图象在![]() 处有相同的切线,求
处有相同的切线,求![]() 的值;
的值;
(2)当![]() 时,若对任意
时,若对任意![]() 和任意
和任意![]() ,总存在不相等的正实数
,总存在不相等的正实数![]() ,使得
,使得![]() ,求
,求![]() 的最小值;
的最小值;
(3)当![]() 时,设函数
时,设函数![]() 与
与![]() 的图象交于
的图象交于![]()
![]() 两点.求证:
两点.求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为2的菱形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.
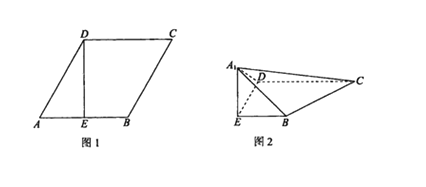
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在这智能手机爆发的时代,大部分高中生都有手机,在手机面前,有些学生无法抵御手机尤其是手机游戏和短视频的诱惑,从而导致无法专心完成学习任务,成绩下滑;但是对于自制力强,能有效管理自己的学生,手机不仅不会对他们的学习造成负面影响,还能成为他们学习的有力助手,我校某研究型学习小组调查研究“中学生使用智能手机对学习的影响”,部分统计数据如表:
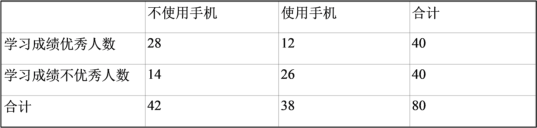
参考数据: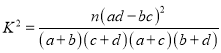 ,其中
,其中![]() .
.
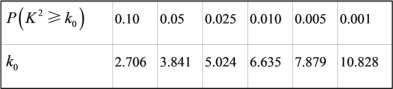
(1)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用手机对学习有影响?
(2)研究小组将该样本中不使用手机且成绩优秀的同学记为![]() 组,使用手机且成绩优秀的同学记为
组,使用手机且成绩优秀的同学记为![]() 组,计划从
组,计划从![]() 组推选的4人和
组推选的4人和![]() 组推选的2人中,随机挑选两人来分享学习经验.求挑选的两人中一人来自
组推选的2人中,随机挑选两人来分享学习经验.求挑选的两人中一人来自![]() 组、另一人来自
组、另一人来自![]() 组的概率.
组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
,![]() ,点P在椭圆上,
,点P在椭圆上,![]() ,椭圆的离心率
,椭圆的离心率![]() .
.
(1)求椭圆C的标准方程;
(2)A,B是椭圆C上与点P不重合的任意两点,若![]() 的重心是坐标原点O,试证明:
的重心是坐标原点O,试证明:![]() 的面积为定值,并求出该定值.
的面积为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数);以原点
为参数);以原点![]() 极点,以
极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
⑴ 求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
⑵ 试判断曲线![]() 与
与![]() 是否存在两个交点,若存在求出两交点间的距离;若不存在,说明理由.
是否存在两个交点,若存在求出两交点间的距离;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com